题目内容
 如图,AD是△ABC的中线,∠ADC=45°,BC=4,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=
如图,AD是△ABC的中线,∠ADC=45°,BC=4,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=考点:翻折变换(折叠问题)
专题:
分析:首先证明∠BDE=90°,借助勾股定理求出DB的长度问题即可解决.
解答: 解:由题意得:△ADC≌△ADE,
解:由题意得:△ADC≌△ADE,
∴DC=DE;∠ADC=∠ADE=45°;
∴∠CDE=90°,
∴∠BDE=90°,
∵AD是△ABC的中线,
∴DB=DC=DE;
由勾股定理得:DB2+DE2=BE2,
即2DB2=BE2,而BE=4,
∴DB=2
,
∴BC=2DB=4
;
故该题答案为4
.
 解:由题意得:△ADC≌△ADE,
解:由题意得:△ADC≌△ADE,∴DC=DE;∠ADC=∠ADE=45°;
∴∠CDE=90°,
∴∠BDE=90°,
∵AD是△ABC的中线,
∴DB=DC=DE;
由勾股定理得:DB2+DE2=BE2,
即2DB2=BE2,而BE=4,
∴DB=2
| 2 |
∴BC=2DB=4
| 2 |
故该题答案为4
| 2 |
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是借助翻折变换的性质找出图形中相等线段或相等的角;然后运用勾股定理等几何知识来分析、判断、推理或解答.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2010-a-b的值是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
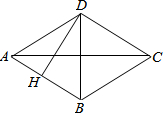 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=axa2-2a-6是二次函数且图象开口向上,则a=( )
| A、-2 | B、4 |
| C、4或-2 | D、4或3 |
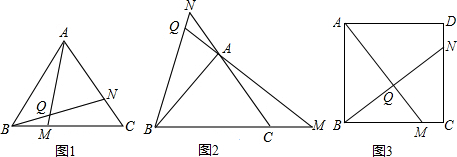
 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为