题目内容
20.如图1所示,在直角梯形ABCD中,AB∥DC,∠B=90°.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图2所示,试求当0≤x≤14时y与x的函数关系式.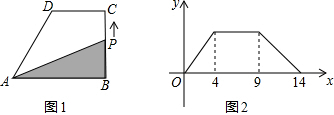
分析 根据图2信息,找到对应的点求出梯形ABCD各边的长,根据3个区间在图1中求出y与x的关系.
解答 解:由题意知:BC=4,DC=9-4=5,AD=5,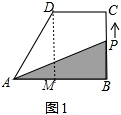
作DM⊥AB垂足为M,
∵四边形ABCD是直角梯形,
∴∠C=∠B=90°,
∵∠DMB=90°,
∴四边形DMBC是矩形,
∴BM=DC=5,DM=BC=4,
在RT△ADM中,AM=$\sqrt{A{D}^{2}-D{M}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AB=AM+BM=8,
当0≤x≤4时,y=$\frac{1}{2}$•AB•PB=$\frac{1}{2}$×8×x=4x,
当4<x≤9时,y=$\frac{1}{2}×AB×BC$=16,
当9<x≤14时,设函数解析式为y=kx+b,
∵经过点(9,16)和(14,0),
∴$\left\{\begin{array}{l}{9k+b=16}\\{14k+b=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{16}{5}}\\{b=\frac{224}{5}}\end{array}\right.$,
∴y=-$\frac{16}{5}$x+$\frac{224}{5}$.
综上所述y=$\left\{\begin{array}{l}{4x}&{(0≤x≤4)}\\{16}&{(4<x≤9)}\\{-\frac{16}{5}x+\frac{224}{5}}&{(9<x≤14)}\end{array}\right.$.
点评 考查了动点问题的函数图象、梯形的有关知识,解决本题的关键是读懂图意,得到相应的直角梯形中各边之间的关系,此题考查了学生从图象中读取信息的数形结合能力.

练习册系列答案
相关题目
10. 反比例函数y=$\frac{k}{x}$(k≠0)的图象在直角坐标系中的位置如图,若点A(-1,y1),B(2,y2),C(3,y3)的在函数y=$\frac{k}{x}$(k≠0)的图象上,则y1,y2,y3的大小关系为( )
反比例函数y=$\frac{k}{x}$(k≠0)的图象在直角坐标系中的位置如图,若点A(-1,y1),B(2,y2),C(3,y3)的在函数y=$\frac{k}{x}$(k≠0)的图象上,则y1,y2,y3的大小关系为( )
 反比例函数y=$\frac{k}{x}$(k≠0)的图象在直角坐标系中的位置如图,若点A(-1,y1),B(2,y2),C(3,y3)的在函数y=$\frac{k}{x}$(k≠0)的图象上,则y1,y2,y3的大小关系为( )
反比例函数y=$\frac{k}{x}$(k≠0)的图象在直角坐标系中的位置如图,若点A(-1,y1),B(2,y2),C(3,y3)的在函数y=$\frac{k}{x}$(k≠0)的图象上,则y1,y2,y3的大小关系为( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y2<y3<y1 |
15.下列说法不正确的是( )
| A. | 9的算术平方根是3 | B. | $\sqrt{16}$的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
7.下列分式中,是最简分式的是( )
| A. | $\frac{x+1}{2(x+1)}$ | B. | $\frac{x-y}{{x}^{2}-{y}^{2}}$ | C. | $\frac{3{x}^{2}+x}{{x}^{2}}$ | D. | $\frac{x+1}{{x}^{2}+1}$ |
 如图,方格纸中每个小方格的边长为1个单位长度,△ABC的顶点都在小方格的顶点上,已知点B的坐标是(4,0),点C的坐标是(1,2).
如图,方格纸中每个小方格的边长为1个单位长度,△ABC的顶点都在小方格的顶点上,已知点B的坐标是(4,0),点C的坐标是(1,2). 如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.
如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O. 如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.