题目内容
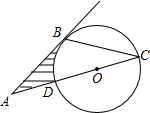 如图,AB为⊙O的切线,切点为点B,切线BA与直径CD的延长线相交于点A,CD=4,∠A=30°,则图中阴影部分的面积为
如图,AB为⊙O的切线,切点为点B,切线BA与直径CD的延长线相交于点A,CD=4,∠A=30°,则图中阴影部分的面积为考点:切线的性质,扇形面积的计算
专题:计算题
分析:连接OB,如图,先根据切线的性质得∠ABO=90°,由CD=4得OB=2,再在Rt△OBA中,根据互余得∠AOB=60°,根据含30度的直角三角形三边的关系得AB=
OB=2
,然后根据扇形面积公式和阴影部分的面积=S△ABO-S扇形DOB进行计算.
| 3 |
| 3 |
解答:解 :连接OB,如图,
:连接OB,如图,
∵AB为⊙O的切线,
∴OB⊥AB,
∴∠ABO=90°,
∵CD=4,
∴OB=2,
在Rt△OBA中,∵∠A=30°,
∴∠AOB=60°,AB=
OB=2
,
∴图中阴影部分的面积=S△ABO-S扇形DOB
=
•2•2
-
=2
-
π.
故答案为2
-
π.
 :连接OB,如图,
:连接OB,如图,∵AB为⊙O的切线,
∴OB⊥AB,
∴∠ABO=90°,
∵CD=4,
∴OB=2,
在Rt△OBA中,∵∠A=30°,
∴∠AOB=60°,AB=
| 3 |
| 3 |
∴图中阴影部分的面积=S△ABO-S扇形DOB
=
| 1 |
| 2 |
| 3 |
| 60•π•22 |
| 360 |
=2
| 3 |
| 2 |
| 3 |
故答案为2
| 3 |
| 2 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
如果等腰三角形的一腰上的高与另一腰的夹角为30°,则该等腰三角形顶角的度数是( )
| A、60° | B、120° |
| C、60°或120° | D、90° |
直径为8的圆内有一点M到圆心O的距离是3,则过点M的弦中,长度为整数的条数为( )
| A、3 | B、4 | C、5 | D、6 |
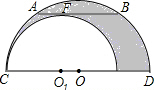 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,则阴影部分的面积是( )| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、4πcm2 |
 如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是
如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是