题目内容
 如图,△ABC中,∠ABC=∠ACB=45°,直线l经过A点,BD⊥l,CE⊥l,垂足分别为D、E,先证明△BDA≌△AEC,然后直接写出BD、DE、EC之间的数量关系.
如图,△ABC中,∠ABC=∠ACB=45°,直线l经过A点,BD⊥l,CE⊥l,垂足分别为D、E,先证明△BDA≌△AEC,然后直接写出BD、DE、EC之间的数量关系.考点:全等三角形的判定与性质
专题:
分析:利用已知得出∠CAE=∠ABD,AB=AC,进而利用AAS得出则△ABD≌△CAE,即可得出BD=AE,AD=CE,再根据等量代换可得DE=BD+CE.
解答:解:DE=BD+CE.
理由如下:
∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°
又∵∠ABC=∠ACB=45°,
∴∠BAC=90°,AB=AC,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD.
理由如下:
∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°
又∵∠ABC=∠ACB=45°,
∴∠BAC=90°,AB=AC,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)
如图,△ABD、△BCE、△ACF均为等边三角形,请回答下列问题(不要求证明)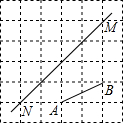 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.