题目内容
 如图,D为△ABC的边AB上的点,请补充一个条件
如图,D为△ABC的边AB上的点,请补充一个条件考点:相似三角形的判定
专题:开放型
分析:已知△ADC和△ACB中有一个公共角,我们可以再添加一个角,从而利用有两组角对应相等的两个三角形相似来判定其相似.
解答:解:∵∠DAC=∠CAB,
∴当∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB时,
均可得出△ADC∽△ACB.
故答案为:∠ADC=∠ACB(∠ACD=∠B或AC2=AD•AB).
∴当∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB时,
均可得出△ADC∽△ACB.
故答案为:∠ADC=∠ACB(∠ACD=∠B或AC2=AD•AB).
点评:本题考查了相似三角形的判定.这是一道开放性的题,答案不唯一.
此题用到的相似三角形的判定定理为:
两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
两角法:有两组角对应相等的两个三角形相似.
此题用到的相似三角形的判定定理为:
两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
自然数3的相反数是( )
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为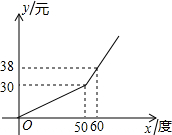 电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电
电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电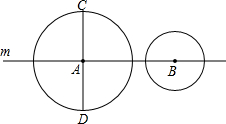 如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是
如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是