题目内容
11.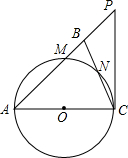 如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.(1)求证:∠BAC=2∠BCP;
(2)若BC=2$\sqrt{5}$,sin∠BCP=$\frac{\sqrt{5}}{5}$,求点B到AC的距离.
分析 (1)连接AN,由圆周角定理可得AN⊥BC,再由等腰三角形的性质可得AN平分∠BAC,所以再证明∠NAC=∠BCP即可;
(2)易求AC,AN的长,再根据△ABC的面积为定值即可得到点B到AC的距离.
解答 (1)证明:连接AN,
∵AC为直径,
∴AN⊥BC,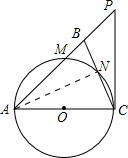
∵AB=AC,
∴AN平分∠BAC,
∵PC是圆的切线,
∴∠ACP=90°,
∵∠NAC+∠ACB=∠PCB+∠ACB=90°,
∴∠NAC=∠BCP,
即∠BAC=2∠BCP;
(2)∵BC=2$\sqrt{5}$,BN=CN,
∴CN=$\sqrt{5}$,
∵sin∠BCP=$\frac{\sqrt{5}}{5}$,
∴sin∠ACN=$\frac{\sqrt{5}}{5}$,
∴AC=5,
∴AN=$\sqrt{A{C}^{2}-C{N}^{2}}$=2$\sqrt{5}$,
∴点B到AC的距离=$\frac{AN•BC}{AC}$=$\frac{2\sqrt{5}×2\sqrt{5}}{5}$=4.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
6.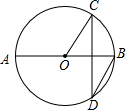 如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
 如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
20.某人的头发的直径约为85微米,已知1微米=0.000001米;则该人头发的直径用科学记数法表示正确的是( )米.
| A. | 8.5×105 | B. | 8.5×10-5 | C. | 85×10-8 | D. | 8.5×10-8 |
 如图,已知等边△ABC,AE=BD,CE,AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:BG+DF=CE.
如图,已知等边△ABC,AE=BD,CE,AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:BG+DF=CE.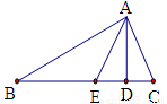
 如图,在平行四边形ABCD中,P、Q是对角线BD上的两个点,且BP=DQ.
如图,在平行四边形ABCD中,P、Q是对角线BD上的两个点,且BP=DQ. 如图,在⊙O中,点C为$\widehat{AB}$的中点,AD=BE,求证:CD=CE.
如图,在⊙O中,点C为$\widehat{AB}$的中点,AD=BE,求证:CD=CE.