题目内容
11.若关于x的二次方程x2+ax+a+3=0有两个相等的实数根,则实数a=-2或6.分析 根据二次方程x2+ax+a+3=0有两个相等的实数根得到△=a2-4(a+3)=0,解一元二次方程求出a的值.
解答 解:∵关于x的二次方程x2+ax+a+3=0有两个相等的实数根,
∴△=0,即a2-4(a+3)=0,
∴a2-4a-12=0,
∴a1=-2,a2=6,
故答案为:-2或6.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△=0,方程有两个相等的实数根,解答此题还需要掌握因式分解法解一元二次方程的步骤,此题难度不大.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.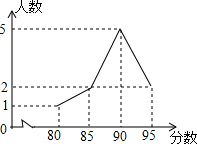 在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
 在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
4. 如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
 如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )| A. | 120m | B. | 100m | C. | 75m | D. | 25m |
6.为增强公民的节水意识,合理利用水资源,某市自1月1日起对市区民用水价格进行调整,实行阶梯式水价,调整后的收费价格如下表所示:
(1)若调价后每月支出的水费为y(元),每月的用水量为x(m3),求y与x之间的函数关系式并注明自变量的取值范围;
(2)若某用户2、3月份共用水16m3(3月份用水高于2月份用水量),共缴费48元,试问该用户2、3月份的用水量各是多少?
| 每月用水量 | 单价 |
| 不超过5m3的部分 | 2 |
| 超过5m3,不超,8m3部分 | 4 |
| 超出8m3部分 | 8 |
(2)若某用户2、3月份共用水16m3(3月份用水高于2月份用水量),共缴费48元,试问该用户2、3月份的用水量各是多少?
2.为求1+2+22+23+…+22015的值,可令S=1+2+22+23+…+22015,则2S=2+22+23+…+22016,因此2S-S=22016-1.仿照以上推理,计算出1+5+52+53+…+52015的值为( )
| A. | 52015-1 | B. | 52016-1 | C. | $\frac{{5}^{2015}-1}{4}$ | D. | $\frac{{5}^{2016}-1}{4}$ |
20.如图所示,已知:$y=\frac{6}{x}$(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).
动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2$\sqrt{3}$,此时P点的坐标为( )
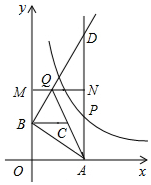
动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2$\sqrt{3}$,此时P点的坐标为( )

| A. | (3,2) | B. | ($\frac{2\sqrt{3}}{3}$,3$\sqrt{3}$) | C. | ($4,\frac{3}{2}$) | D. | ($\frac{4\sqrt{3}}{5}$,$\frac{5\sqrt{3}}{2}$) |
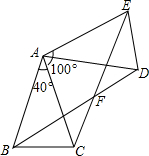 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地,设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示.根据图象回答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地,设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示.根据图象回答下列问题: .
.