题目内容
6.已知关于x的方程(1)x2-(1-2a)x+a2-3=0有两个不相等的实数根,且关于x的方程(2)x2-2x+2a-1=0没有实数根,问a取什么整数时,方程(1)有整数解.分析 若一元二次方程有两不等根,则根的判别式△=b2-4ac>0,建立关于a的不等式,求出a的取值范围;关于x的方程②x2-2x+2a-1=0没有实数根,则根的判别式△=b2-4ac<0,建立关于a的不等式,求出a的取值范围;解关于a的不等式组,再求a的范围.
解答 解:∵方程①有两个不相等的实数根,
∴△=b2-4ac=[-(1-2a)]2-4×(a2-3)=13-4a>0,
解得:a<$\frac{13}{4}$,
又∵方程②没有实数根,
∴△=b2-4ac=(-2)2-4×1×(2a-1)=8-8a<0,
解得:a>1,
∴a取的整数值有2,3,
当a=2时,方程①变为x2+3x+1=0,无整数实根;
当a=3时,方程②变为x2+5x+6=0,有整数实根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
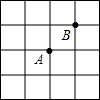 已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数有多少?并在图中标出C点的位置.
已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数有多少?并在图中标出C点的位置.