题目内容
16.已知关于x的方程x2-(k+2)x+2k=0(1)求证:无论k取何值,方程总有实数根;
(2)若等腰△ABC的边长a=3,另两边长b,c恰好是这个方程的两个根,△ABC的周长.
分析 (1)根据一元二次方程的根的判别式的符号进行证明;
(2)分b=c,b=a两种情况探讨得出答案即可.
解答 (1)证明:△=[-(k+2)]2-4×1×2k=(k-2)2,
∵无论k取何值,(k-2)2≥0,即△≥0,
∴无论k取任何实数,方程总有实数根;
(2)解:①当b=c时,则△=0,
即(k-2)2=0,
∴k=2,
方程可化为x2-4x+4=0,
∴x1=x2=2,
而b=c=2,
∴△ABC的周长=a+b+c=3+2+2=7;
②解:当b=a=3时,
∵x2-(k+2)x+2k=0.
∴(x-2)(x-k)=0,
∴x=2或x=k,
∵另两边b、c恰好是这个方程的两个根,
∴k=b=3,
∴c=2,
∴△ABC的周长=a+b+c=3+3+2=8;
综上所述,△ABC的周长为7或8.
点评 本题考查了根的判别式的运用,等腰三角形的性质,注意分类讨论思想的渗透.

练习册系列答案
相关题目
11.在△ABC中,AB=AC.
(1)若D为AC的中点,BD把三角形的周长分别24cm和30cm两部分,求△ABC三边的长.
(2)若D为AC上一点,试说明AC>$\frac{1}{2}$(BD+DC)
(1)若D为AC的中点,BD把三角形的周长分别24cm和30cm两部分,求△ABC三边的长.
(2)若D为AC上一点,试说明AC>$\frac{1}{2}$(BD+DC)
5.-(-2)的值是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 4 |
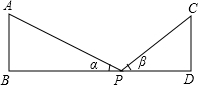 如图,在水平地面上有两座高度相同的高压电缆,铁搭AB和CD两塔底B和D之间的距离为87米,在两塔底连结BD上取一点P,测得两塔顶A和C的仰角分别为α和β,如果tanα=$\frac{3}{4}$,tanβ=$\frac{12}{13}$,求铁搭的高度.
如图,在水平地面上有两座高度相同的高压电缆,铁搭AB和CD两塔底B和D之间的距离为87米,在两塔底连结BD上取一点P,测得两塔顶A和C的仰角分别为α和β,如果tanα=$\frac{3}{4}$,tanβ=$\frac{12}{13}$,求铁搭的高度.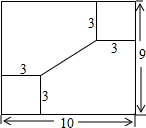 如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.
如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.