题目内容
19.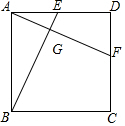 如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
分析 根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE和△ADF全等,由此即可证明.
解答 证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠D=90°}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠AEG=90°,
∴∠DAF+∠AEG=90°,
∴∠AGE=90°,
∴BE⊥AF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.

练习册系列答案
相关题目
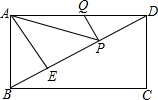 如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为$\frac{9}{2}$.
如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为$\frac{9}{2}$.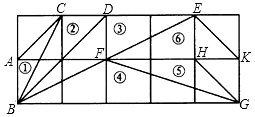 如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.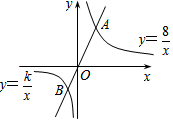 如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$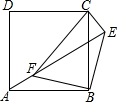 如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.
如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.