题目内容
 如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.
如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.考点:勾股定理,含30度角的直角三角形
专题:
分析:延长AD与BC,两延长线交于点E,由∠B=∠D=90°,得到三角形ABE与三角形CDE都为直角三角形,由∠A=60°,得到∠E=30°,在直角三角形CDE中,利用30°所对的直角边等于斜边的一半,根据CD的长求出DE的长,同理在直角三角形ABE中,由AB的长求出AE的长,用AE-DE求出AD的长,用BE-CE求出BC的长即可.
解答: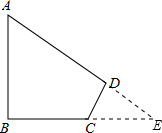 解:延长AD与BC,两延长线交于点E,如图所示,
解:延长AD与BC,两延长线交于点E,如图所示,
∵∠B=90°,∠A=60°,
∴∠E=30°,
在Rt△CDE中,CD=1,
∴CE=2CD=2,
根据勾股定理得:DE=
=
,
在Rt△ABE中,AB=2,
∴AE=2AB=4,
根据勾股定理得:BE=
=2
,
则BC=BE-CE=2
-2,AD=AE-DE=4-
.
 解:延长AD与BC,两延长线交于点E,如图所示,
解:延长AD与BC,两延长线交于点E,如图所示,∵∠B=90°,∠A=60°,
∴∠E=30°,
在Rt△CDE中,CD=1,
∴CE=2CD=2,
根据勾股定理得:DE=
| CE2-CD2 |
| 3 |
在Rt△ABE中,AB=2,
∴AE=2AB=4,
根据勾股定理得:BE=
| AE2-AB2 |
| 3 |
则BC=BE-CE=2
| 3 |
| 3 |
点评:此题考查了勾股定理,以及含30°直角三角形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?
如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱? 如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.
如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积. 如图,平行四边形ABCD的面积为36,对角线AC,BD交于点O点,E为CD上一点,已知四边形EFOG的面积为3,则阴影部分的面积为
如图,平行四边形ABCD的面积为36,对角线AC,BD交于点O点,E为CD上一点,已知四边形EFOG的面积为3,则阴影部分的面积为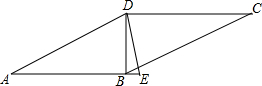 如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.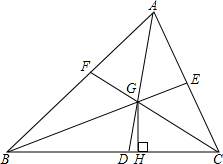 如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.
如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.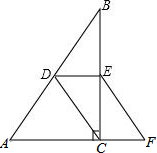 如图,在△ABC中,∠ACB=90°,DE是△ABC的中位线,点F在AC的延长线上,且CF=
如图,在△ABC中,∠ACB=90°,DE是△ABC的中位线,点F在AC的延长线上,且CF=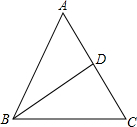 如图,已知AB=AC,BC=BD=DA.
如图,已知AB=AC,BC=BD=DA.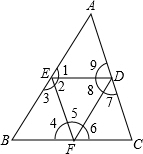 如图,填空:
如图,填空: