题目内容
18.若a2=b2,且ab<0,b和c互为倒数,则(a+b)3-(-bc)1003=1.分析 由a2=b2,且ab<0,可知a、b互为相反数,从而得到a+b=0,由倒数的定义可知bc=1,然后代入计算即可.
解答 解:∵a2=b2,
∴a=b或a=-b.
∵ab<0,
∴a=-b.
∴a+b=0.
∵b和c互为倒数,
∴bc=1.
∴原式=03-(-1)1003=0-(-1)=0+1=1.
故答案为:1.
点评 本题主要考查的是求代数式的值,求得a+b=0,bc=1是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.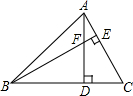 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
8.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2015的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | (-3)2015 |
 画出如图所示几何体的三视图.
画出如图所示几何体的三视图.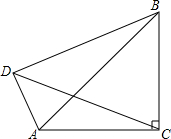 如图,△ABC中,AC=BC,∠ACB=90°,D为△ABC外一点,且∠CDB=45°,
如图,△ABC中,AC=BC,∠ACB=90°,D为△ABC外一点,且∠CDB=45°,