题目内容
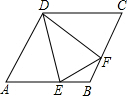 已知如图,在菱形ABCD中,EF分别是AB和BC上的点,且BE=BF,求证:
已知如图,在菱形ABCD中,EF分别是AB和BC上的点,且BE=BF,求证:(1)△ADE≌△CDF;
(2)∠DEF=∠DFE.
考点:菱形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据菱形的性质和全等三角形的判定方法“SAS”即可证明△ADE≌△CDF;
(2)由(1)可知△ADE≌△CDF,所以DE=DF,进而得到∠DEF=∠DFE.
(2)由(1)可知△ADE≌△CDF,所以DE=DF,进而得到∠DEF=∠DFE.
解答:证明:(1)
∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
(SAS),
∴△ADE≌△CDF;
(2)∵△ADE≌△CDF,
∴DE=DF,
∴∠DEF=∠DFE.
∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
|
∴△ADE≌△CDF;
(2)∵△ADE≌△CDF,
∴DE=DF,
∴∠DEF=∠DFE.
点评:本题是简单的推理证明题,主要考查菱形的边的性质,同时综合利用全等三角形的判定方法及等腰三角形的性质.

练习册系列答案
相关题目
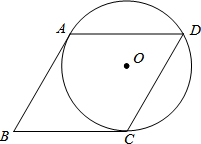 如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°.
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°. 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.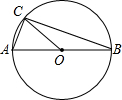 (1)现有两组相同的扑克牌,每组两张,两张牌的牌面数字分别是2和3,从每组牌中各随机摸出一张牌,如果摸到的牌面数字相同小红获胜,否则小明获胜,请用列表法或画树状图的方法说明这个游戏是否公平?
(1)现有两组相同的扑克牌,每组两张,两张牌的牌面数字分别是2和3,从每组牌中各随机摸出一张牌,如果摸到的牌面数字相同小红获胜,否则小明获胜,请用列表法或画树状图的方法说明这个游戏是否公平?