题目内容
8.△ABC的周长为12,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、DF,则△DEF的周长是6.分析 利用三角形的中位线定理可以得到:DE=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$BC,则△DEF的周长是△ABC的周长的一半,据此即可求解.
解答 解:∵D、E分别是△ABC的边AB、BC的中点,
∴DE=$\frac{1}{2}$AC,
同理,EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$BC,
∴C△DEF=DE+EF+DF=$\frac{1}{2}$AC+$\frac{1}{2}$BC+$\frac{1}{2}$AB=$\frac{1}{2}$(AC+BC+AC)=$\frac{1}{2}$×12=6.
故答案是:6.
点评 本题考查了三角形的中位线定理,正确根据三角形中位线定理证得:△DEF的周长是△ABC的周长的一半是关键.

练习册系列答案
相关题目
20.单项式-xy2( )
| A. | 系数是0,次数是3 | B. | 系数是-1,次数是2 | ||
| C. | 系数是1,次数是2 | D. | 系数是-1,次数是3 |
18.在一次献爱心捐赠活动中,某班45名同学捐款金额统计如下:
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 10 | 13 | 5 | 15 | 2 |
| A. | 15,13 | B. | 15,30 | C. | 50,30 | D. | 50,35 |
 如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.
如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.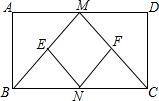 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.