题目内容
5．解不等式组：$\left\{\begin{array}{l}{x+3≤2x}\\{\frac{x+1}{3}＞\frac{x}{2}-1}\end{array}\right.$．分析 首先解每个不等式，两个不等式解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{x+3≤2x…①}\\{\frac{x+1}{3}＞\frac{x}{2}-1…②}\end{array}\right.$，
解①得x≥3，
解②得x＜8．
则不等式组的解集是：3≤x＜8．
点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
19．从1、2、3、4四个整数中任取两个数作为一个点的坐标，那么这个点恰好在抛物线y=x2上的概率是（ ）
| A． | $\frac{1}{24}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
16．根据等式的性质，下列变形正确的是（ ）
| A． | 若2x=a，则x=2a | B． | 若$\frac{x}{2}$+$\frac{x}{3}$=1，则3x+2x=1 | ||
| C． | 若ab=bc，则a=c | D． | 若$\frac{a}{c}$=$\frac{b}{c}$，则a=b |
13．
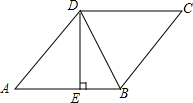如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，BE=2，则tan∠DBE的值是（ ）
如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，BE=2，则tan∠DBE的值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | 10$\sqrt{3}$ | D． | $\frac{\sqrt{5}}{5}$ |
20．
如图所示几何体的俯视图是（ ）
如图所示几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
如图，有3张不透明的卡片，除正面写有不同的数字外，其他均相同，将这3张卡片背面向上洗匀，从中随机抽取一张，记下数字后放回；重新洗匀后再从中随机抽取一张，将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数，请用画树状图（或列表）的方法，求这个两位数能被3整除的概率．