题目内容
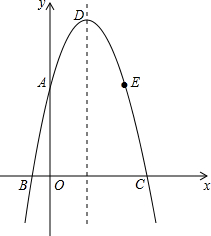 如图,开口向下顶点为D的抛物线经过点A(0,5),B(-1,0),C(5,0)与x轴交于B、C两点(B在C左侧),点A和点E关于抛物线对称轴对称.
如图,开口向下顶点为D的抛物线经过点A(0,5),B(-1,0),C(5,0)与x轴交于B、C两点(B在C左侧),点A和点E关于抛物线对称轴对称.(1)求该抛物线的解析式;
(2)经过原点O和点E的直线与抛物线的另一个交点为F.
①求点F的坐标;
②求四边形ADEF的面积;
(3)若M为抛物线上一动点,N为抛物线对称轴上一动点,是否存在M,N,使得以A、E、M、N为顶点的四边形为平行四边形?若存在,求出所有满足条件的M、N的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)可将抛物线的解析式设成交点式,然后用待定系数法就可求出抛物线的解析式.
(2)①可先求出直线OE的解析式,然后将直线OE与抛物线的解析式联立,组成方程组,解这个方程组就可得到点F的坐标;
②只需运用割补法就可求出四边形ADEF的面积.
(3)可分AE是平行四边形的对角线和一边这两种情况讨论,然后利用平行四边形的性质就可解决问题.
(2)①可先求出直线OE的解析式,然后将直线OE与抛物线的解析式联立,组成方程组,解这个方程组就可得到点F的坐标;
②只需运用割补法就可求出四边形ADEF的面积.
(3)可分AE是平行四边形的对角线和一边这两种情况讨论,然后利用平行四边形的性质就可解决问题.
解答:解:(1)如图1,
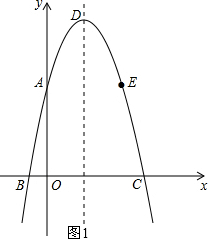
由于抛物线经过点B(-1,0),C(5,0),
因此该抛物线解析式可设为y=a(x+1)(x-5),
把A(0,5)代入y=a(x+1)(x-5),
得-5a=5,
解得:a=-1,
∴y=-(x+1)(x-5)=-x2+4x+5 …2分
(2)①如图2,
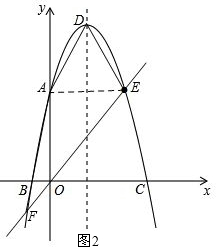
∵抛物线的对称轴x=-
=2,点A(0,5)和点E关于抛物线对称轴对称,
∴点E的坐标为(4,5),
∴直线OE的解析式为y=
x,
解方程组
,
得
,或
,
∴点F坐标为(-
,-
)
②∵y=-x2+4x+5=-(x-2)2+9,
∴抛物线的顶点D的坐标为(2,9),
∴S四边形ADEF=S△ADE+S△AEF
=
×4×(9-5)+
×4×(5+
)=
(3)①若AE是平行四边形的对角线,如图3①,
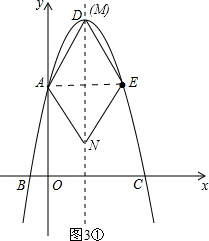
则点M在对称轴上,即在顶点D处,
此时点M的坐标(2,9),点N的坐标为(2,1);
②若AE是平行四边形的一边,如图3①,
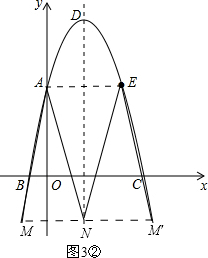
则有MN=AE=4,
∴点M的横坐标为-2或6.
Ⅰ.当x=-2时,y=-(-2)2+4×(-2)+5=-7,
此时点M的坐标为(-2,-7),点N的坐标为(2,-7);
Ⅱ.当x=6时,y=-62+4×6+5=-7,
此时点M的坐标为(6,-7),点N的坐标为(2,-7).
综上所述:符合要求的点M、N的坐标为
M1(-2,-7),M2(6,-7),M3(2,9)
N1(2,-7),N2(2,-7),N3(2,1).
(注:没过程,写对点的坐标酌情扣1~2 分)

由于抛物线经过点B(-1,0),C(5,0),
因此该抛物线解析式可设为y=a(x+1)(x-5),
把A(0,5)代入y=a(x+1)(x-5),
得-5a=5,
解得:a=-1,
∴y=-(x+1)(x-5)=-x2+4x+5 …2分
(2)①如图2,

∵抛物线的对称轴x=-
| 4 |
| 2×(-1) |
∴点E的坐标为(4,5),
∴直线OE的解析式为y=
| 5 |
| 4 |
解方程组
|
得
|
|
∴点F坐标为(-
| 5 |
| 4 |
| 25 |
| 16 |
②∵y=-x2+4x+5=-(x-2)2+9,
∴抛物线的顶点D的坐标为(2,9),
∴S四边形ADEF=S△ADE+S△AEF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 16 |
| 169 |
| 8 |
(3)①若AE是平行四边形的对角线,如图3①,

则点M在对称轴上,即在顶点D处,
此时点M的坐标(2,9),点N的坐标为(2,1);
②若AE是平行四边形的一边,如图3①,

则有MN=AE=4,
∴点M的横坐标为-2或6.
Ⅰ.当x=-2时,y=-(-2)2+4×(-2)+5=-7,
此时点M的坐标为(-2,-7),点N的坐标为(2,-7);
Ⅱ.当x=6时,y=-62+4×6+5=-7,
此时点M的坐标为(6,-7),点N的坐标为(2,-7).
综上所述:符合要求的点M、N的坐标为
M1(-2,-7),M2(6,-7),M3(2,9)
N1(2,-7),N2(2,-7),N3(2,1).
(注:没过程,写对点的坐标酌情扣1~2 分)
点评:本题考查了用待定系数法求抛物线的解析式、求直线与抛物线的交点坐标、抛物线的性质、平行四边形的性质等知识,运用割补法是解决第(2)②小题的关键,运用分类讨论的思想是解决第(3)小题的关键.

练习册系列答案
相关题目
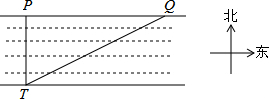 如图,为了测量一条河流的宽度,一测量员在河岸边相距180m的P和Q两点分别测定对岸一棵树T的位置,T在P的正南方向,在Q的南偏西50°的方向,求河宽(结果精确到 1m).
如图,为了测量一条河流的宽度,一测量员在河岸边相距180m的P和Q两点分别测定对岸一棵树T的位置,T在P的正南方向,在Q的南偏西50°的方向,求河宽(结果精确到 1m).
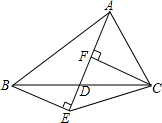 已知点D是BC的中点,BE⊥AD,CF⊥AD,垂足分别为E、F,试判断四边形BECF是不是平行四边形,并证明你的结论.
已知点D是BC的中点,BE⊥AD,CF⊥AD,垂足分别为E、F,试判断四边形BECF是不是平行四边形,并证明你的结论.