题目内容
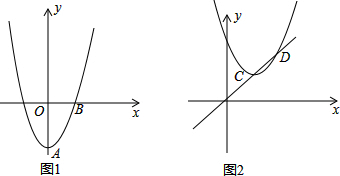
如图1,在平面直角坐标系中,抛物线C1:y=ax2-a2(a>0)经过点B(1,0),顶点为A
(1)求抛物线C1的解析式;
(2)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C2,设抛物线C2与直线y=x交于C、D两点,求线段CD的长;
(3)在图1中将抛物线C1绕点B旋转180°后得到抛物线C3,直线y=kx-2k+4总经过一定点M,若过定点M的直线l与抛物线C3只有一个公共点,求直线l的解析式.
(1)求抛物线C1的解析式;
(2)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C2,设抛物线C2与直线y=x交于C、D两点,求线段CD的长;
(3)在图1中将抛物线C1绕点B旋转180°后得到抛物线C3,直线y=kx-2k+4总经过一定点M,若过定点M的直线l与抛物线C3只有一个公共点,求直线l的解析式.

考点:二次函数综合题
专题:
分析:(1)把点B(1,0)代入y=ax2-a2,可得出a的值,即可求出抛物线C1的解析式;
(2)设抛物线C2的顶点为(m,m),依题意可得抛物线C2的解析式为:y=(x-m)2+m,与直线y=x联立,可得C,D的坐标,过点C作CM∥x轴,过点D作DM∥y轴,可求出CM=1,DM=1,即可得出CD的值.
(3)依题意可求出抛物线C3的解析式为:y=-(x-2)2+1,由直线y=kx-2k+4总经过一定点M,可求得定点M为(2,4),①经过定点M(2,4),与y轴平行的直线l:x=2与抛物线C3总有一个公共点(2,1).②经过定点M(2,4)的直线l为一次函数y=kx-2k+4时,与y=-(x-2)2+1联立方程组,利用△=k2-12=0,可得得k1,k2的值,即可得出y=2
x+4-4
或y=-2
x+4+4
,综上所述,过定点M,共有三条直线它们分别与抛物线C3只有一个公共点.
(2)设抛物线C2的顶点为(m,m),依题意可得抛物线C2的解析式为:y=(x-m)2+m,与直线y=x联立,可得C,D的坐标,过点C作CM∥x轴,过点D作DM∥y轴,可求出CM=1,DM=1,即可得出CD的值.
(3)依题意可求出抛物线C3的解析式为:y=-(x-2)2+1,由直线y=kx-2k+4总经过一定点M,可求得定点M为(2,4),①经过定点M(2,4),与y轴平行的直线l:x=2与抛物线C3总有一个公共点(2,1).②经过定点M(2,4)的直线l为一次函数y=kx-2k+4时,与y=-(x-2)2+1联立方程组,利用△=k2-12=0,可得得k1,k2的值,即可得出y=2
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:(1)把点B(1,0)代入y=ax2-a2,得0=a-a2,解得a=0,或1,
∵a>0,
∴a=1,
∴y=x2-1.
(2)设抛物线C2的顶点为(m,m),依题意抛物线C2的解析式为:y=(x-m)2+m,
与直线y=x联立
,
解方程组得:
,
,
∴C(m,m),D(m+1,m+1)
过点C作CM∥x轴,过点D作DM∥y轴,
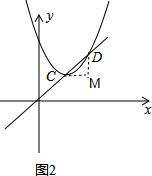
∴CM=1,DM=1,
∴CD=
.
(3)依题意可求出抛物线C3的解析式为:y=-(x-2)2+1,
∵直线y=kx-2k+4总经过一定点M,
∴定点M为(2,4),
①经过定点M(2,4),与y轴平行的直线l:x=2与抛物线C3总有一个公共点(2,1).
②经过定点M(2,4)的直线l为一次函数y=kx-2k+4时,与y=-(x-2)2+1联立方程组,消去y得x2-4x+3+kx-2k+4=0,
即x2-(4-k)x+7-2k=0,△=k2-12=0,得k1=2
,k2=-2
,
∴y=2
x+4-4
或y=-2
x+4+4
,
综上所述,过定点M,共有三条直线l:x=2 或y=2
x+4-4
或y=-2
x+4+4
,它们分别与抛物线C3只有一个公共点.
∵a>0,
∴a=1,
∴y=x2-1.
(2)设抛物线C2的顶点为(m,m),依题意抛物线C2的解析式为:y=(x-m)2+m,
与直线y=x联立
|
解方程组得:
|
|
∴C(m,m),D(m+1,m+1)
过点C作CM∥x轴,过点D作DM∥y轴,

∴CM=1,DM=1,
∴CD=
| 2 |
(3)依题意可求出抛物线C3的解析式为:y=-(x-2)2+1,
∵直线y=kx-2k+4总经过一定点M,
∴定点M为(2,4),
①经过定点M(2,4),与y轴平行的直线l:x=2与抛物线C3总有一个公共点(2,1).
②经过定点M(2,4)的直线l为一次函数y=kx-2k+4时,与y=-(x-2)2+1联立方程组,消去y得x2-4x+3+kx-2k+4=0,
即x2-(4-k)x+7-2k=0,△=k2-12=0,得k1=2
| 3 |
| 3 |
∴y=2
| 3 |
| 3 |
| 3 |
| 3 |
综上所述,过定点M,共有三条直线l:x=2 或y=2
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程:①5x=6x-7y;②
+x=1;③x2=3x;④x=0;⑤2x-5=7.其中,属于一元一次方程的有( )
| 8 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
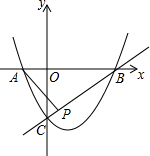 已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.
已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.下列计算中,正确的是( )
A、2
| ||||||||||
B、(
| ||||||||||
C、(3+2
| ||||||||||
D、(
|
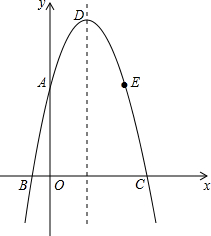 如图,开口向下顶点为D的抛物线经过点A(0,5),B(-1,0),C(5,0)与x轴交于B、C两点(B在C左侧),点A和点E关于抛物线对称轴对称.
如图,开口向下顶点为D的抛物线经过点A(0,5),B(-1,0),C(5,0)与x轴交于B、C两点(B在C左侧),点A和点E关于抛物线对称轴对称.