题目内容
7.在数学里,我们规定:a-n=$\frac{1}{{a}_{n}}$(a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=$\frac{1}{a}$.数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+$\frac{1}{3}$i=$\frac{7}{3}$i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6×0.5i; 2i×3i=6i2=-6;(3i)2=9i2=9;-4的平方根为±2i;如果x2=-7,那么x=±$\sqrt{7}$i.…数的不断发展进一步证实,这种规定是合理的.
利用上述所学知识解决下面的两个问题:
(1)解方程:x2+5=0;
(2)试用配方法求一元二次方程x2+x+1=0的非实数解.
分析 (1)移项得x2=-5,根据阅读材料求出x=±$\sqrt{5}$i;
(2)先将原式配方后变为(x+$\frac{1}{2}$)2=-$\frac{3}{4}$,再将x+$\frac{1}{2}$当作一个整体按照条件中的方法就可以求出其值.
解答 解:(1)x2+5=0,
x2=-5,
x=±$\sqrt{5}$i,
x1=$\sqrt{5}$i,x2=-$\sqrt{5}$i;
(2)原方程变形为:(x+$\frac{1}{2}$)2=-$\frac{3}{4}$,
∴x+$\frac{1}{2}$=±$\frac{\sqrt{3}}{2}$i,
∴x1=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,x2=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i.
点评 本题考查了一元二次方程的运用以及解法,在解答中要求学生具有较强的阅读能力和分析能力,解决现实生活中的实际问题.

练习册系列答案
相关题目
17.已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2-7x+10=0的两根,则直线a与圆的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相离 | D. | 相离 |
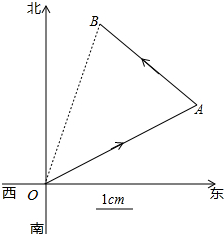 如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.
如图,一只蚂蚁从点O出发,沿北偏东60°方向爬行4cm后到达A地,后折向西北方向爬行3cm到达B点.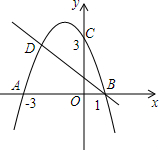 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.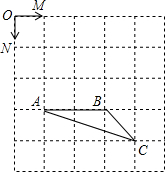 如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.