题目内容
16．
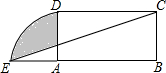如图，在矩形ABCD中，AB=8cm，BC=4cm，以点A为圆心，AD为半径作圆与BA的延长线交于点E，连接CE，则阴影部分的面积是4π-$\frac{8}{3}$cm2．
分析 设AD与CE相交于点F，根据CD∥AE可得出△CDF∽△EAF，由相似三角形的性质求出AF的长，再根据S阴影=S扇形EAD-S△AEF即可得出结论．
解答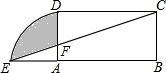 
解：设AD与CE相交于点F，
∵在矩形ABCD中，AB=8cm，BC=4cm，CD∥AE，
∴△CDF∽△EAF，
∴$\frac{AE}{CD}$=$\frac{AF}{AD}$，即$\frac{4}{8}$=$\frac{AF}{4-AF}$，解得AF=$\frac{4}{3}$，
∴S阴影=S扇形EAD-S△AEF=$\frac{90π×{4}^{2}}{360}$-$\frac{1}{2}$×4×$\frac{4}{3}$=4π-$\frac{8}{3}$．
故答案为：4π-$\frac{8}{3}$．
点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
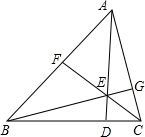如图，在△ABC中，AD、BG、CF交于点E，则$\frac{EF}{CF}$+$\frac{EG}{BG}$+$\frac{ED}{AD}$=1．
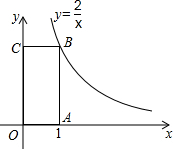如图，点B在反比例函数y=$\frac{2}{x}$（x＞0）的图象上，过B分别向x轴，y轴作垂线，垂足分别为A，C，则矩形OABC的面积为（ ）
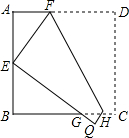如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则△EBG的周长是12cm．