题目内容
8.已知正方形ABCD的边长为2,点P是直线CD上一点,若DP=1,则tan∠PBC的值是$\frac{1}{2}$或$\frac{3}{2}$.分析 本题可以利用锐角三角函数的定义、勾股定理以及正方形的性质求解.
解答 解:此题有两种可能: (1)∵BC=2,DP=1,
(1)∵BC=2,DP=1,
∠C=90°,
∴tan∠PBC=$\frac{PC}{BC}=\frac{1}{2}$;
(2)∵DP=1,DC=2,
∴PC=3,
又∵BC=2,∠C=90°,
∴tan∠PBC=$\frac{PC}{BC}=\frac{3}{2}$,
故答案为:$\frac{1}{2}$或$\frac{3}{2}$;
点评 本题考查了锐角三角函数的定义、勾股定理以及正方形的性质,解题的关键是利用图形考虑此题有两种可能,要依次求解.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
19.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a2)3=a6 | C. | (-2a)2=4a2 | D. | a10÷a2=a5 |
3.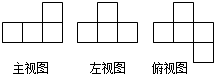 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
20.下列商标是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
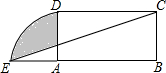 如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.
如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.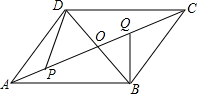 ?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.
?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.