题目内容
1.题目:已知实数a,x满足a>2且x>2,试判断ax与a+x的大小关系,并加以说明.思路:可用“求差法”比较两个数的大小,先列出ax与a+x的差y=ax-(a+x),再说明y的符号即可.
简解:可将y的代数式整理成y=(a-1)x-a,要判断y的符号可借助函数y=(a-1)x-a的图象和性质解决.
参考以上解题思路解以下问题:
已知a,b,c都是非负数,a<5,且a2-a-2b-2c=0,a+2b-2c+3=0
(1)分别用含a的代数式表示4b,4c.
(2)根据条件,写出a的取值范围.
(3)理解阅读材料中蕴含的数学思想,试说明a,b,c之间的大小关系.
分析 (1)根据a2-a-2b-2c=0,a+2b-2c+3=0,整理得出4b=a2-2a-3.
(2)利用4(b-a)=a2-6a-3=(a-3)2-12,得出二次函数的图象即可,再利用4(c-a)=a2-4a+3=(a-1)(a-3),得出图象,进而得出a,b,c大小关系.
解答 解:(1)∵a2-a-2b-2c=0,a+2b-2c+3=0,
∴$\left\{\begin{array}{l}{2b+2c={a}^{2}-a}\\{2c-2b=a+3}\end{array}\right.$,
消去b并整理,得 4c=a2+3.
消去c并整理,得4b=a2-2a-3.
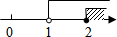
(2)∵4b=a2-2a-3=(a-1)2-4,将4b看成a的函数,结合图象1,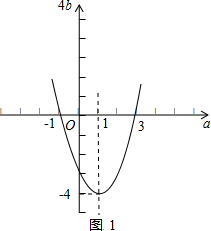
由a,b均非负数,
∴a≥3,
又∵a<5,
∴3≤a<5.
(3)∵4(b-a)=a2-6a-3=(a-3)2-12,
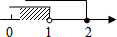
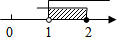
将4(b-a)看成a的函数,由函数4(b-a)=(a-3)2-12的性质结合它的图象(如图2所示)可知,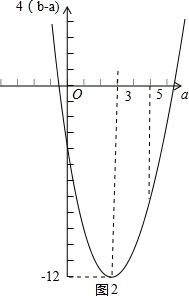
当3≤a<5时,4(b-a)<0.
∴b<a.
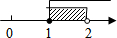
∵4(c-a)=a2-4a+3=(a-1)(a-3),a≥3,
∴4(c-a)≥0.
∴c≥a.
∴b<a≤c.
点评 此题主要考查了二次函数的性质以及利用二次函数图象得出a,b,c大小关系,利用数形结合是这部分考查的重点.

练习册系列答案
相关题目
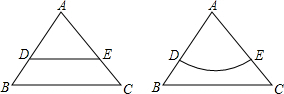 如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”)
如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”)
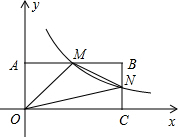 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.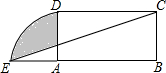 如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.
如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.