题目内容
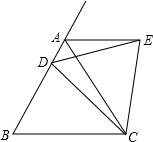 如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.
如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.(1)△DBC和△EAC全等吗?说说你的理由.
(2)求证:AE∥BC.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质得出BC=AC,DC=EC,∠BCA=∠ECD=60°,从而得出∠BCD=∠ACE,利用SAS判定△BDC≌△AEC;
(2)根据△BDC≌△AEC得∠EAC=∠CBD=60°,再由∠ACB=60°,即可得出AE∥BC.
(2)根据△BDC≌△AEC得∠EAC=∠CBD=60°,再由∠ACB=60°,即可得出AE∥BC.
解答:解:(1)△BDC≌△AEC.理由如下:
∵△ABC、△EDC均为等边三角形,
∴BC=AC,DC=EC,∠BCA=∠ECD=60°.
从而∠BCD=∠ACE.
在△BDC和△AEC中,
,
∴△BDC≌△AEC(SAS);
(2)∵△BDC≌△AEC,
∴∠EAC=∠CBD,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠EAC=60°,
∴∠EAC=∠CBD,
∴AE∥BC.
∵△ABC、△EDC均为等边三角形,
∴BC=AC,DC=EC,∠BCA=∠ECD=60°.
从而∠BCD=∠ACE.
在△BDC和△AEC中,
|
∴△BDC≌△AEC(SAS);
(2)∵△BDC≌△AEC,
∴∠EAC=∠CBD,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠EAC=60°,
∴∠EAC=∠CBD,
∴AE∥BC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
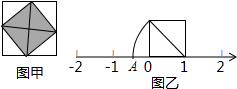 根据图甲,在图乙的数轴上以1个单位长度的线段为边作一个正方形,以表示数1的点为圆心,以正方形对角线长为半径画弧,交数轴负半轴于点A,点A所表示的数是( )
根据图甲,在图乙的数轴上以1个单位长度的线段为边作一个正方形,以表示数1的点为圆心,以正方形对角线长为半径画弧,交数轴负半轴于点A,点A所表示的数是( )A、-1-
| ||
B、1-
| ||
C、
| ||
D、1-
|
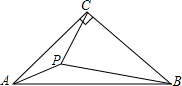 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )| A、105° | B、120° |
| C、135° | D、150° |
 如图所示,四边形ABCD中,DC∥AB,BC=2,AB=AC=AD=
如图所示,四边形ABCD中,DC∥AB,BC=2,AB=AC=AD=| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知两个相似多边形的相似比是3:4,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A、48cm | B、54cm |
| C、56cm | D、64cm |
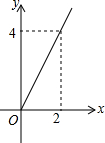 王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为
王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为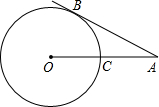 如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.
如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.