题目内容
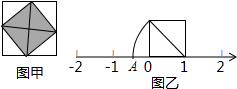 根据图甲,在图乙的数轴上以1个单位长度的线段为边作一个正方形,以表示数1的点为圆心,以正方形对角线长为半径画弧,交数轴负半轴于点A,点A所表示的数是( )
根据图甲,在图乙的数轴上以1个单位长度的线段为边作一个正方形,以表示数1的点为圆心,以正方形对角线长为半径画弧,交数轴负半轴于点A,点A所表示的数是( )A、-1-
| ||
B、1-
| ||
C、
| ||
D、1-
|
考点:勾股定理,实数与数轴
专题:
分析:先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式为:两点间的距离=较大的数-较小的数,便可求出1和A之间的距离,进而可求出点A表示的数.
解答:解:数轴上正方形的对角线长为:
=
,由图中可知1和A之间的距离为
.
∴点A表示的数是1-
.
故选B.
| 12+12 |
| 2 |
| 2 |
∴点A表示的数是1-
| 2 |
故选B.
点评:本题考查的是勾股定理及两点间的距离公式,本题需注意:知道数轴上两点间的距离,求较小的数,就用较大的数减去两点间的距离.

练习册系列答案
相关题目
在相似的两个三角形,已知其中一个三角形的三边长是4、6、8,另一个三角形最短的一边长是2,则另一个三角形的周长是( )
| A、4.5 | B、6 |
| C、9 | D、以上答案都有可能 |
 如图,某环形的大圆半径是5米,小圆半径是3米,则该环形的面积是
如图,某环形的大圆半径是5米,小圆半径是3米,则该环形的面积是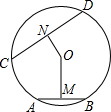 如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB>CD,OM和ON的大小有什么关系?为什么?
如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB>CD,OM和ON的大小有什么关系?为什么?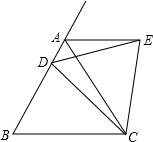 如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.
如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.