题目内容
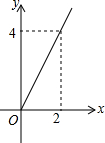 王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为
王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为
|
(1)求王亮解题的学习收益量y与用于解题的时间x之间的函数关系式,并写出自变量x的取值范围;
(2)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?
(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
考点:二次函数的应用
专题:
分析:(1)设y=kx代入(2,4)可得k与y的值.15≤x≤30;
(2)学习效益总量为W,根据题意可得W=-(x-4)2+76可推出z随着x的增大而减小.
(2)学习效益总量为W,根据题意可得W=-(x-4)2+76可推出z随着x的增大而减小.
解答:解:(1)设y=kx,把(2,4)代入,
得:k=2.
∴y=2x.
自变量x的取值范围是:
15≤x≤30.
(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,
则他用于解题的时间为(30-x)分钟.
当0≤x≤5时,W=-x2+10x+2(30-x)=-x2+8x+60=-(x-4)2+76.
∴当x=4时,W最大=76.
当5<x≤15时,W=25+2(30-x)=-2x+85.
∵W随x的增大而减小,
∴当x=5时,W最大=75
综合所述,当x=4时,W最大=76,此时30-x=26.
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
得:k=2.
∴y=2x.
自变量x的取值范围是:
15≤x≤30.
(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,
则他用于解题的时间为(30-x)分钟.
当0≤x≤5时,W=-x2+10x+2(30-x)=-x2+8x+60=-(x-4)2+76.
∴当x=4时,W最大=76.
当5<x≤15时,W=25+2(30-x)=-2x+85.
∵W随x的增大而减小,
∴当x=5时,W最大=75
综合所述,当x=4时,W最大=76,此时30-x=26.
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
点评:本题考查了待定系数法求一次函数的解析式的运用,二次函数的运用,顶点式求二次函数的最大值的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,不正确是( )
| A、若a>2,则a-2>0 |
| B、若a>2,则2-a<0 |
| C、若ac2>bc2,则a>b |
| D、若a>b,则ac2>bc2 |
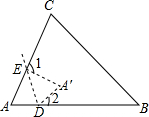 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE重叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )| A、120° | B、110° |
| C、100° | D、80° |
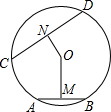 如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB>CD,OM和ON的大小有什么关系?为什么?
如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB>CD,OM和ON的大小有什么关系?为什么?
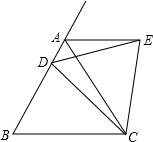 如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.
如图,等边△ABC中,D是AB边上动点,作等边△EDC,连AE.