题目内容
如图,C和D分别是⊙O的半径OA和弦AB上的点,且CD⊥OA,点E在CD的延长线上,且ED=EB.
(1)求证:BE与⊙O相切;
(2)如图2,已知AC=2OC,△DEB为等边三角形,若BE=
,求⊙O的半径.

(1)求证:BE与⊙O相切;
(2)如图2,已知AC=2OC,△DEB为等边三角形,若BE=
| 3 |

考点:切线的判定
专题:综合题
分析:(1)连接OB,如图1所示,由CD与OA垂直,得到∠ACD为直角,进而得到两个角互余,由OA=OB,ED=EB,利用等边对等角分别得到两对角相等,等量代换得到OB与BE垂直,由OB为圆的半径,即可得证;
(2)连接OB,过O作OF垂直于AB,利用垂径定理得到F为AB中点,由AC=2OC,设AC=2k,OC=k,表示出半径OA=3k,由三角形BDE为等边三角形,得到三条边相等,三个角为60度,得到∠OAF为30度,利用30度角所对的直角边等于斜边的一半表示出OF,在直角三角形ACD中,利用锐角三角函数定义表示出AD,由AD+DB表示出AB,进而表示出FB,在直角三角形OBF中,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可确定出圆O的半径.
(2)连接OB,过O作OF垂直于AB,利用垂径定理得到F为AB中点,由AC=2OC,设AC=2k,OC=k,表示出半径OA=3k,由三角形BDE为等边三角形,得到三条边相等,三个角为60度,得到∠OAF为30度,利用30度角所对的直角边等于斜边的一半表示出OF,在直角三角形ACD中,利用锐角三角函数定义表示出AD,由AD+DB表示出AB,进而表示出FB,在直角三角形OBF中,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可确定出圆O的半径.
解答: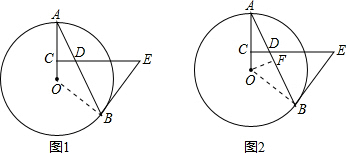 (1)证明:连接OB,如图1所示,
(1)证明:连接OB,如图1所示,
∵CD⊥OA,
∴∠ACD=90°,
∴∠OAB+∠ADC=90°,
∵DE=BE,OA=OB,
∴∠OAB=∠ABO,∠EBD=∠EDB=∠ADC,
∴∠ABO+∠EBD=90°,
即OB⊥BE,
∵OB为半径,
∴BE与⊙O相切;
(2)解:过O作OF⊥AB,交AB于点F,得到F为AB中点,连接OB,如图2所示,
由AC=2OC,且AC+CO=OA,设AC=2k,则OC=k,OA=3k,
∵△BDE为等边三角形,
∴BD=BE=DE=
,∠BDE=∠ADC=60°,
在Rt△ACD中,∠ACD=90°,
∴∠BAF=30°,AD=
=
k,
∴AB=AD+DB=
+
k,
∴FB=
AB=
+
k,
在Rt△AOF中,∠OAF=30°,
∴OF=
OA=
k,
在Rt△BOF中,根据勾股定理得:OB2=OF2+FB2,
即(3k)2=
k2+(
+
k)2,
整理得:(5k-3)(13k+3)=0,
解得:k=
或k=-
(舍去),
则圆的半径为3k=
.
 (1)证明:连接OB,如图1所示,
(1)证明:连接OB,如图1所示,∵CD⊥OA,
∴∠ACD=90°,
∴∠OAB+∠ADC=90°,
∵DE=BE,OA=OB,
∴∠OAB=∠ABO,∠EBD=∠EDB=∠ADC,
∴∠ABO+∠EBD=90°,
即OB⊥BE,
∵OB为半径,
∴BE与⊙O相切;
(2)解:过O作OF⊥AB,交AB于点F,得到F为AB中点,连接OB,如图2所示,
由AC=2OC,且AC+CO=OA,设AC=2k,则OC=k,OA=3k,
∵△BDE为等边三角形,
∴BD=BE=DE=
| 3 |
在Rt△ACD中,∠ACD=90°,
∴∠BAF=30°,AD=
| AC |
| cos30° |
4
| ||
| 3 |
∴AB=AD+DB=
| 3 |
4
| ||
| 3 |
∴FB=
| 1 |
| 2 |
| ||
| 2 |
2
| ||
| 3 |
在Rt△AOF中,∠OAF=30°,
∴OF=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△BOF中,根据勾股定理得:OB2=OF2+FB2,
即(3k)2=
| 9 |
| 4 |
| ||
| 2 |
2
| ||
| 3 |
整理得:(5k-3)(13k+3)=0,
解得:k=
| 3 |
| 5 |
| 3 |
| 13 |
则圆的半径为3k=
| 9 |
| 5 |
点评:此题考查了切线的判定,锐角三角函数定义,勾股定理,垂径定理,以及特殊角的三角函数值,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
 已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C.
已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C. 某航船以20海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东45°处,半小时后航行到B处,此时灯塔Q与航船的距离最短.
某航船以20海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东45°处,半小时后航行到B处,此时灯塔Q与航船的距离最短. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟?
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟? 如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
