题目内容
某航船以20海里/时的速度向正北方向航行，在A处看灯塔Q在航船北偏东45°处，半小时后航行到B处，此时灯塔Q与航船的距离最短．（1）请你在图中画出点B的位置；
（2）求灯塔Q到A处的距离．（精确到0.1海里）
考点：勾股定理的应用
专题：
分析：（1）过点Q向AB作垂线，AB的长即为所求；
（2）利用勾股定理求出AQ的长．
（2）利用勾股定理求出AQ的长．
解答：
解：（1）点B如图所求．
（2）依题意得：QB⊥AB，∠BAQ=45°，AB=10，
在Rt△ABQ中，∠ABQ=90°，∠BQA=∠BAQ=45°，
∴BA=BQ=10，
∴AQ=
=
≈14.1（海里），
答：灯塔Q到A处的距离约为14.1海里．
解：（1）点B如图所求．（2）依题意得：QB⊥AB，∠BAQ=45°，AB=10，
在Rt△ABQ中，∠ABQ=90°，∠BQA=∠BAQ=45°，
∴BA=BQ=10，
∴AQ=
| BA2+BQ2 |
| 102+102 |
答：灯塔Q到A处的距离约为14.1海里．
点评：本题考查了勾股定理，找到合适的量代入公式即可求解．
练习册系列答案
相关题目
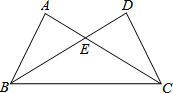如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．
如图，△ABC中，AB=AC，∠A=40°
已知抛物线经过点A（-3，0）、B（1，0）、C（0，3）．