题目内容
如图①,已知线段AB=8,以AB为直径作半圆O,再以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D.
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=60°时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.

(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=60°时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.

考点:圆的综合题
专题:
分析:(1)AP=PD.理由如下:如图①,连接OP.利用圆周角定理知OP⊥AD.然后由等腰三角形“三合一”的性质证得AP=PD;
(2)如图①,连接PC、OD.通过证PC∥OD推知∠AOD=∠ACP=60°,所以根据弧长公式得到:弧AD的长=
=
π;
(3)分类讨论:点E落在线段OA和线段OB上,这两种情况下的y与x的关系式.这两种情况都是根据相似三角形(△APO∽△AED)的对应边成比例来求y与x之间的函数关系式的.
(2)如图①,连接PC、OD.通过证PC∥OD推知∠AOD=∠ACP=60°,所以根据弧长公式得到:弧AD的长=
| 60×π×4 |
| 180 |
| 4 |
| 3 |
(3)分类讨论:点E落在线段OA和线段OB上,这两种情况下的y与x的关系式.这两种情况都是根据相似三角形(△APO∽△AED)的对应边成比例来求y与x之间的函数关系式的.
解答: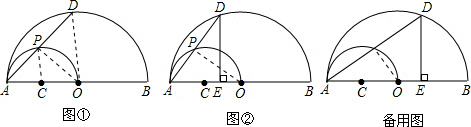 解:(1)AP=PD
解:(1)AP=PD
理由如下:连接OP、OD.
∵OA是半圆C的直径,
∴∠APO=90°,即OP⊥AD.
又∵OA=OD,
∴AP=PD;
(2)如图①,连接PC、OD.
由(1)知,AP=PD.
又∵AC=OC,
∴PC∥OD,
∴∠AOD=∠ACP=60°,
∵AB=8,∴OA=4
∴弧AD的长=
=
π;
(3)分两种情况:①如图②,当点E落在OA上(即0<x≤2
时)
连接OP,则∠APO=∠AED
又∵∠A=∠A
∴△APO∽△AED
∴
=
∵AP=x,AO=4,AD=2x,AE=4-y
∴
=
∴y=-
x2+4(0<x≤2
)
②如备用图,当点E落在线段OB上(即2
<x<4)时,连接OP
同①可得,△APO∽△AED
∴
=
∵AP=x,AO=4,AD=2x,AE=4+y
∴
=
∴y=
x2-4(2
<x<4).
 解:(1)AP=PD
解:(1)AP=PD理由如下:连接OP、OD.
∵OA是半圆C的直径,
∴∠APO=90°,即OP⊥AD.
又∵OA=OD,
∴AP=PD;
(2)如图①,连接PC、OD.
由(1)知,AP=PD.
又∵AC=OC,
∴PC∥OD,
∴∠AOD=∠ACP=60°,
∵AB=8,∴OA=4
∴弧AD的长=
| 60×π×4 |
| 180 |
| 4 |
| 3 |
(3)分两种情况:①如图②,当点E落在OA上(即0<x≤2
| 2 |
连接OP,则∠APO=∠AED
又∵∠A=∠A
∴△APO∽△AED
∴
| AP |
| AE |
| AO |
| AD |
∵AP=x,AO=4,AD=2x,AE=4-y
∴
| x |
| 4-y |
| 4 |
| 2x |
∴y=-
| 1 |
| 2 |
| 2 |
②如备用图,当点E落在线段OB上(即2
| 2 |
同①可得,△APO∽△AED
∴
| AP |
| AE |
| AO |
| AD |
∵AP=x,AO=4,AD=2x,AE=4+y
∴
| x |
| 4+y |
| 4 |
| 2x |
∴y=
| 1 |
| 2 |
| 2 |
点评:本题综合考查了圆周角定理、圆的切线的性质以及相似三角形的判定与性质.解答(3)题时,要分类讨论,以防漏解.解答几何问题时,要数形结合,使抽象的问题变得形象化,降低题的难度与梯度.

练习册系列答案
相关题目


 已知抛物线经过点A(-3,0)、B(1,0)、C(0,3).
已知抛物线经过点A(-3,0)、B(1,0)、C(0,3).