题目内容
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟?
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟?考点:一次函数的应用
专题:
分析:y1=20x-200(40≤x≤60),y2=100x-4000(40≤x≤50),当y1=y2时,兔子追上乌龟,此时20x-200=100x-4000,解得:x=47.5,所以y1=y2=750米,即兔子在途中750米处追上乌龟.
解答:解:如图,设y1=k1x+b(k1≠0)(40≤x≤60).
根据图示知,该直线经过点(40,600),(60,1000),
则
,
解得,
,
所以该函数解析式为y1=20x-200(40≤x≤60),
同理,y2=100x-4000(40≤x≤50),
当y1=y2时,兔子追上乌龟,
此时20x-200=100x-4000,
解得:x=47.5,
所以y1=y2=750米,即兔子在途中750米处追上乌龟.
答:兔子在途中750米处追上乌龟.
根据图示知,该直线经过点(40,600),(60,1000),
则
|
解得,
|
所以该函数解析式为y1=20x-200(40≤x≤60),
同理,y2=100x-4000(40≤x≤50),
当y1=y2时,兔子追上乌龟,
此时20x-200=100x-4000,
解得:x=47.5,
所以y1=y2=750米,即兔子在途中750米处追上乌龟.
答:兔子在途中750米处追上乌龟.
点评:本题考查了一次函数的应用.读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程,有一定难度.

练习册系列答案
相关题目
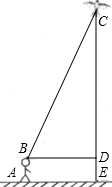 八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:
八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作: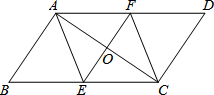 如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F.
如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F. 如图,在平面直角坐标系中,抛物线y1=
如图,在平面直角坐标系中,抛物线y1=
 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD. 如图,在平面内有A、B、C三点.
如图,在平面内有A、B、C三点.