题目内容
20．若α、β是方程x2+2x-2015=0的两个实数根，则α2+3α+β的值为（ ）| A． | 2015 | B． | B、2013 | C． | -2015 | D． | 4030 |
分析 先根据一元二次方程的解的定义得到α2+2α-2015=0，则α2+2α=2015，于是α2+3α+β可化为2015+α+β，再利用根与系数的关系得到α+β=-2，然后利用整体代入的方法计算．
解答 解：∵α是方程x2+2x-2015=0的根，
∴α2+2α-2015=0，
∴α2+2α=2015，
∴α2+3α+β=2015+α+β，
∵α、β是方程x2+2x-2015=0的两个实数根，
∴α+β=-2，
∴α2+3α+β=2015-2=2013．
故选B．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程的解．
练习册系列答案
ABC考王全优卷系列答案
相关题目
10．
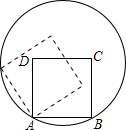如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为（ ）
如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为（ ）| A． | 2$\sqrt{2}$π | B． | （$\sqrt{2}$+1）π | C． | （$\sqrt{2}$+2）π | D． | （$\frac{2}{3}$$\sqrt{2}$+1）π |
12．已知关于x的一元二次方程ax2+bx+c=3的一根为x=2，且二次函数y=ax2+bx+c的对称轴是直线x=2，则抛物线的顶点坐标是（ ）
| A． | （2，3） | B． | （2，1） | C． | （2，-3） | D． | （3，2） |
如图（1），直线y=-x+3分别与y轴、x轴交于A、C两点，以OA、OC为边作正方形OABC，E是边OC上一点，将直线AE绕A点逆时针旋转45°与过E点垂直于AE的直线交于点D．