题目内容
 已知:如图,⊙O的直径AB=2,BC与⊙O交于点D,∠ABC=30°,BC=2
已知:如图,⊙O的直径AB=2,BC与⊙O交于点D,∠ABC=30°,BC=2| 3 |
(1)求证:BD=CD;
(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.
考点:切线的判定
专题:证明题
分析:(1)求出∠ADB=90°,求出BD,求出CD,即可得出答案;
(2)连接OD,求出OD∥AC,推出DE⊥OD,根据切线的判定推出即可.
(2)连接OD,求出OD∥AC,推出DE⊥OD,根据切线的判定推出即可.
解答:(1)证明: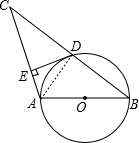 连接AD,
连接AD,
∵AB是⊙O直径,
∴∠ADB=90°,
∵AB=2,∠ABC=30°,
∴AD=
AB=1,由勾股定理得:BD=
,
∵BC=2
,
∴CD=2
-
=
,
即BD=CD.
(2)证明:连接OD,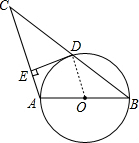
∵BD=CD,AO=BO,
∴OD∥AC,
∵DE⊥AC,
∴OC⊥DE,
∵OD为半径,
∴直线DE是⊙O的切线.
 连接AD,
连接AD,∵AB是⊙O直径,
∴∠ADB=90°,
∵AB=2,∠ABC=30°,
∴AD=
| 1 |
| 2 |
| 3 |
∵BC=2
| 3 |
∴CD=2
| 3 |
| 3 |
| 3 |
即BD=CD.
(2)证明:连接OD,

∵BD=CD,AO=BO,
∴OD∥AC,
∵DE⊥AC,
∴OC⊥DE,
∵OD为半径,
∴直线DE是⊙O的切线.
点评:本题考查了切线的判定,平行线的判定和性质,勾股定理,含30度角的直角三角形,三角形的中位线的应用,主要考查学生的推理能力,题目比较好.

练习册系列答案
相关题目
抛一枚普通硬币10次,其中4次出现正面,则出现正面的频率为( )
| A、2.5 | B、1.6 |
| C、0.6 | D、0.4 |
从分别写有数字“-
、-
、1、
、3、π”的六张一样的卡片中,任意抽取一张卡片,则所抽卡片上数字的绝对值小于3的概率是( )
| 5 |
| 3 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 某幼儿园为了增加幼儿的安全性,决定将园内滑梯的倾斜角由60°降为45°,原滑梯AB长为2米,考虑滑梯的正前面要留有空地保证安全性,滑梯的底部BC不动,只有将滑梯的高度降低,滑梯的高度应该降低多少米?(参考数据
某幼儿园为了增加幼儿的安全性,决定将园内滑梯的倾斜角由60°降为45°,原滑梯AB长为2米,考虑滑梯的正前面要留有空地保证安全性,滑梯的底部BC不动,只有将滑梯的高度降低,滑梯的高度应该降低多少米?(参考数据