题目内容
已知抛物线y=x2-（a+2）x+4的顶点在坐标轴上，求a的值．
考点：二次函数的性质
专题：
分析：由于抛物线的顶点在坐标轴上，故应分在x轴上与y轴上两种情况进行讨论．
解答：解：当抛物线y=x2-（a+2）x+4的顶点在x轴上时，△=0，即△=（a+2）2-4×4=0，解得a=2或a=-6；
当抛物线y=x2-（a+2）x+4的顶点在y轴上时，x=
=0，解得a=-2．
故a的值为2或-6或-2．
当抛物线y=x2-（a+2）x+4的顶点在y轴上时，x=
| a+2 |
| 2 |
故a的值为2或-6或-2．
点评：本题考查的是二次函数的性质，解答此题时要注意进行分类讨论，不要漏解．
练习册系列答案
相关题目
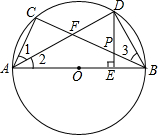如图，△ABC内接于⊙O，AB为直径，∠CAB的平分线交BC于点F，交⊙O于点D，DE⊥AB于点E，且交BC于点P，BF=如果a＞b＞0，c＞d＞0，则一定有（ ）
| A、ab-cd＞0 |
| B、bc-ad＞0 |
| C、cd-ab＞0 |
| D、ac-bd＞0 |
已知线段AB，求作线段OC，使OC=AB．
如图，在△ABC中，AD是BC边上的中线，sinB=
如图，点O是△ABC内任意一点，连接AO、BO、CO，点E、F、D分别是BO、CO、AO的中点，求证：△EDF∽△BAC．