Question

4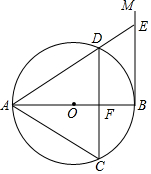．如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD∥BM，交AB于点F，且$\widehat{DA}$=$\widehat{DC}$，连接AC，AD，延长AD交BM于点E．
（1）求证：△ACD是等边三角形；
（2）连接OE，若⊙O的半径为2，求OE的值．

Answer 1

分析 （1）由AB是⊙O的直径，过点B作⊙O的切线BM，易得BE⊥AB，又由弦CD∥BM，可得AB⊥CD，又由且$\widehat{DA}$=$\widehat{DC}$，即可得$\widehat{AD}$=$\widehat{AC}$=$\widehat{CD}$，继而证得结论；
（2）由△ACD是等边三角形，CD⊥AB，可求得BE的长，继而求得答案．

解答 （1）证明：∵AB是⊙O的直径，BM是⊙O的切线，
∴AB⊥BE，
∵弦CD∥BM，
∴CD⊥AB，
∴$\widehat{AD}$=$\widehat{AC}$，
∵$\widehat{DA}$=$\widehat{DC}$，
∴$\widehat{AD}$=$\widehat{AC}$=$\widehat{CD}$，
∴AD=AC=CD，
∴△ACD是等边三角形；

（2）解：由（1）知，△ACD是等边三角形，
∴∠DAC=60°，
∵AD=AC，CD⊥AB，
∴∠DAB=30°，
∴BE=$\frac{1}{2}$AE，
∵OA=OB=r=2，
在Rt△ABE中，AE²=AB²+BE²，
∴BE²=$\frac{16}{3}$，
在Rt△OBE中，OE²=2²+$\frac{16}{3}$=$\frac{28}{3}$，
∴OE=$\frac{2\sqrt{21}}{3}$．

点评 此题考查了切线的性质、垂径定理、等边三角形的判定与性质以及勾股定理．注意掌握切线的性质是关键．