题目内容
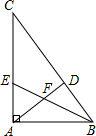 在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.
在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.考点:等腰三角形的判定与性质
专题:证明题
分析:由△ABC中,∠BAC=90°,AD⊥BC与FB平分∠ABC,根据等角的余角相等,易得∠AFE=∠BED,又由对顶角相等,可得∠AEF=∠AFE,则可证得AE=AF.
解答:证明:∵△ABC中,∠BAC=90°,
∴∠ABE+∠AEB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠FBD+∠BFD=90°,
∵EB平分∠ABC,
∴∠ABE=∠FBD,
∴∠BFD=∠AEF,
∵∠BFD=∠AFE,
∴∠AFE=∠AEF,
∴AE=AF.

∴∠ABE+∠AEB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠FBD+∠BFD=90°,
∵EB平分∠ABC,
∴∠ABE=∠FBD,
∴∠BFD=∠AEF,
∵∠BFD=∠AFE,
∴∠AFE=∠AEF,
∴AE=AF.
点评:此题考查了等腰三角形的判定以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
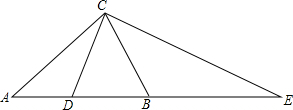 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
 如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=
如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
用同样大小的黑色五角星按图所示的方式摆图案,按照这样的规律摆下去,第13个图案需要的黑色五角星的个数是( )


| A、18 | B、19 | C、21 | D、22 |
 如图,在四边形ABCD中,∠A-∠B=∠C-∠D,求证:AB∥CD.
如图,在四边形ABCD中,∠A-∠B=∠C-∠D,求证:AB∥CD. 如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.
如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积. 如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.
如图,在△ABC中,AB=AC,AD是△ABC的中线,BE平分∠ABC交AD于点E,连接EC.求证:CE平分∠ACB.