题目内容
8.①计算|-2|+($\sqrt{3}+1}$)0+2sin30°-($\frac{1}{2}}$)-1②先化简,再求值:(a+$\frac{1-2a}{a}$)÷$\frac{1-a}{a}$,其中a=1-$\sqrt{2}$.
分析 ①根据绝对值、零指数幂、锐角三角函数和负整数指数幂可以解答本题;
②先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:①|-2|+($\sqrt{3}+1}$)0+2sin30°-($\frac{1}{2}}$)-1
=2+1+2×$\frac{1}{2}$-2
=2+1+1-2
=2;
②(a+$\frac{1-2a}{a}$)÷$\frac{1-a}{a}$
=$\frac{{a}^{2}-2a+1}{a}×\frac{a}{1-a}$
=$\frac{(a-1)^{2}}{1-a}$
=1-a,
当a=1-$\sqrt{2}$时,原式=1-(1-$\sqrt{2}$)=$\sqrt{2}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列计算正确的是( )
| A. | (x2)3=x5 | B. | x6+x6=x12 | C. | x2•x3=x5 | D. | (2x)2=2x2 |
17.下列给出的各组线段中,能构成三角形的是( )
| A. | 5,12,13 | B. | 5,12,7 | C. | 8,18,7 | D. | 3,4,8 |
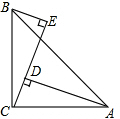 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=25,BE=8,求DE的长.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=25,BE=8,求DE的长.