题目内容
2.解方程:(1)x2+3x-2=0;
(2)(x+1)(x-1)=2$\sqrt{2}x$;
(3)$\frac{x+2}{3}$-$\frac{{x}^{2}-3}{2}$=2.
分析 (1)方程利用公式法求出解即可;
(2)方程整理后,利用配方法求出解即可;
(3)方程整理后,利用因式分解法求出解即可.
解答 解:(1)这里a=1,b=3,c=-2,
∵△=9+8=17,
∴x=$\frac{-3±\sqrt{17}}{2}$,
解得:x1=$\frac{-3+\sqrt{17}}{2}$,x2=$\frac{-3-\sqrt{17}}{2}$;
(2)方程整理得:x2-2$\sqrt{2}$x=1,
配方得:x2-2$\sqrt{2}$x+2=3,即(x-$\sqrt{2}$)2=3,
开方得:x-$\sqrt{2}$=±$\sqrt{3}$,
解得:x1=$\sqrt{2}$+$\sqrt{3}$,x2=$\sqrt{2}$-$\sqrt{3}$;
(3)方程整理得:2x+4-3x2+9=12,即3x2-2x-1=0,
分解因式得:(3x+1)(x-1)=0,
解得:x1=-$\frac{1}{3}$,x2=1.
点评 此题考查了解一元二次方程-因式分解法,公式法,以及配方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
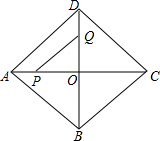 如图,在菱形ABCD中,AD=5,AC=6,对角线AC,BD交于点O,P.Q分别是线段AO,DO上的动点,P从A出发以1cm速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.
如图,在菱形ABCD中,AD=5,AC=6,对角线AC,BD交于点O,P.Q分别是线段AO,DO上的动点,P从A出发以1cm速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.