题目内容
20.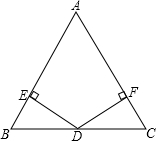 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.(1)BE、CF有怎样的数量关系?证明你的结论;
(2)若∠A=90°,求证:四边形DFAE是正方形.
分析 (1)证明△BED≌△CFD,由全等三角形的性质可知BE=CF;
(2)首先证明四边形DFAE为矩形,然后由△BED≌△CFD可知DE=DF,从而可证明四边形DFAE为正方形.
解答 (1)答:BE=CF.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,
∴∠B=∠C.
∵D是BC的中点,
∴BD=CD.
在△BED和△CFD中,$\left\{\begin{array}{l}{∠BED=∠CFD=90°}\\{∠B=∠C}\\{BD=CD}\end{array}\right.$
∴△BED≌△CFD.
∴BE=CF.
(2)解:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE为矩形.
∵△BED≌△CFD.
∴DE=DF.
∴四边形DFAE为正方形.
点评 本题主要考查的是等腰三角形的性质、全等三角形的性质和判定、矩形的判定和正方形的判定,掌握相关定理是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
15.在一个暗箱里放有a个除颜色外其他完全相同的球,这a个球中红球有4个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在0.25,那么可以推算出a大约是( )
| A. | 3 | B. | 4 | C. | 12 | D. | 16 |
12.“m的$\frac{1}{3}$与n的差”用代数式表示为( )
| A. | $\frac{1}{3}(m-n)$ | B. | $m-\frac{1}{3}-n$ | C. | $\frac{1}{3}m-n$ | D. | $m-\frac{1}{3}n$ |
9.下列是矩形与菱形都具有的性质的是( )
| A. | 各角都相等 | B. | 各边都相等 | C. | 对角线相等 | D. | 有两条对称轴 |