题目内容
4.阅读下面的文字,解答问题:大家知道$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部地写出来,于是小明用$\sqrt{2}$-1来表示$\sqrt{2}$的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为$\sqrt{2}$的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵$\sqrt{4}$<$\sqrt{7}$<$\sqrt{9}$,即2<$\sqrt{7}$<3,∴$\sqrt{7}$的整数部分为2,小数部分为($\sqrt{7}$-2).
请解答:
(1)如果$\sqrt{5}$的小数部分a=$\sqrt{5}$-2,$\sqrt{13}$的整数部分b=3,则a+b-$\sqrt{5}$=1;
(2)已知:10+$\sqrt{3}$=x+y,其中整数部分x=11,且0<y<1,求x-y的值.
分析 (1)分别求出$\sqrt{5}$和$\sqrt{13}$的范围,求出a、b的值即可;
(2)求出$\sqrt{3}$的范围,即可求出x和x-y的值.
解答 解:(1)∵2<$\sqrt{5}$<3,3<$\sqrt{13}$<4,
∴a=$\sqrt{5}$-2,b=3,
a+b-$\sqrt{5}$=$\sqrt{5}$-2+3-$\sqrt{5}$=1,
故答案为:$\sqrt{5}$-2,3,1;
(2)∵1<$\sqrt{3}$<2,10+$\sqrt{3}$=x+y,
∴x=11,y=10+$\sqrt{3}$-11=$\sqrt{3}$-1,
x-y=11-($\sqrt{3}$-1)=12-$\sqrt{3}$,
故答案为:11.
点评 本题考查了估算无理数的大小,能估算出$\sqrt{13}$、$\sqrt{3}$和$\sqrt{5}$的范围是解此题的关键.

练习册系列答案
相关题目
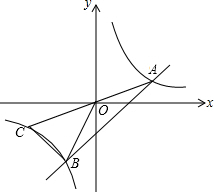 如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.
如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.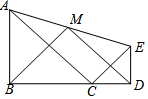 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,