题目内容
17.下列函数中,是反比例函数的是( )| A. | y=$\frac{x}{2}$ | B. | y=-$\frac{\sqrt{3}}{3x}$ | C. | y=$\frac{2}{{x}^{2}}$ | D. | y=1-$\frac{1}{x}$ |
分析 根据反比例函数的定义,反比例函数的一般式是y=$\frac{k}{x}$(k≠0),即可判断各函数类型是否符合题意.
解答 解:A、y与x是正比例函数关系,故本选项错误;
B、y=-$\frac{\sqrt{3}}{3x}$,符合反比例函数解析式的一般形式,故本选项正确;
C、y与x2是反比例函数,故本选项错误;
D、y=1-$\frac{1}{x}$=$\frac{x-1}{x}$,不符合反比例函数解析式的一般形式,故本选项错误;.
故选:B.
点评 本题考查了反比例函数的定义,重点是掌握反比例函数解析式的一般式y=$\frac{k}{x}$(k≠0).

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 数据4,6,5,2,-1的中位数是4 | |
| B. | 从2,3,4,5,6中随机抽一个数,是奇数的可能性比较大 | |
| C. | 若甲组数据的方差S甲2=0.71,乙组数据的方差S乙2=0.92,则甲组数据比乙组数据小 | |
| D. | 若某种游戏活动的中奖率为35%,则参加这种活动100次必有35次中奖 |
5.若m>n,则下列不等式成立的是( )
| A. | -3m>-2n | B. | am>an | C. | a2m>a2n | D. | m-3>n-3 |
2.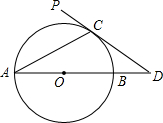 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )| A. | 2$\sqrt{2}$-2 | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
6.“2x-1=x+●”是一个被墨水污染过的方程,答案显示次方程的解是x=3,被墨水遮盖的是一个常数,则这个常数是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
7.下列三个说法中:
(1)两点确定一条直线;
(2)同角(等角)的补角相等;
(3)两点之间,直线最短.
其中正确的个数是( )
(1)两点确定一条直线;
(2)同角(等角)的补角相等;
(3)两点之间,直线最短.
其中正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.
如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.