题目内容
5.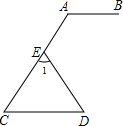 如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.
如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.
分析 由AB∥CD,∠A=120°,根据两直线平行同旁内角互补,可求∠C的度数,然后根据三角形内角和定理即可求出∠D的度数.
解答 解:∵AB∥CD,∠A=120°,
∴∠A+∠C=180°,
∴∠C=60°,
∵∠C+∠D+∠1=180°,∠1=72°,
∴∠D=180°-60°-72°=48°.
点评 此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.

练习册系列答案
相关题目
17.已知二次函数y=x2-2mx+m2+3(m为常数),下列结论正确的是( )
| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 | |
| D. | 该函数图象沿y轴向下平移6个单位后,图象与x轴两交点之间的距离为2$\sqrt{3}$ |
15.下列运算中正确的是( )
| A. | 3a+2a=5a2 | B. | (2a2)3=8a6 | C. | 2a2•a3=2a6 | D. | (2a+b)2=4a2+b2 |
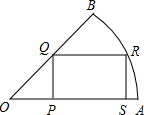 如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.
如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR. 如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.
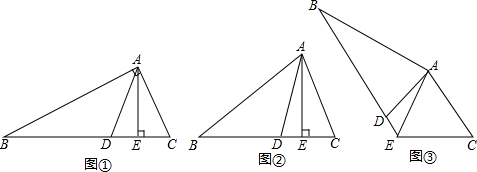
如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.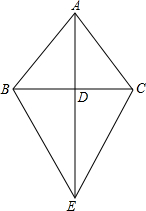 如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.
如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.