题目内容
16.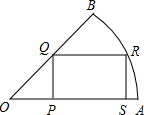 如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.
如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.(1)当∠AOR=30°时,求OP的长;
(2)设OP=x,OS=y,求y与x的函数关系及定义域.
分析 如图,扇形中,连结OR.
(1)根据含30°的直角三角形的性质可求RS,再根据矩形的性质可得PQ,再根据等腰直角三角形的性质即可求解;
(2)先根据等腰直角三角形的性质表示出PQ,根据矩形的性质表示出RS,再根据勾股定理即可得到y与x的函数关系及定义域.
解答 解:如图,扇形中,连结OR.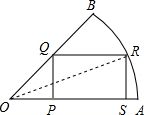
(1)∵∠AOR=30°时,
∴RS=$\frac{1}{2}$OR=1,
∵四边形PQRS是矩形,
∴PQ=RS=1,
∵∠AOB=45°,
∴OP=PQ=1;
(2)∵∠AOB=45°,
∴OP=PQ=x;
∵四边形PQRS是矩形,
∴PQ=RS=x,
在Rt△ORS中,OS2+RS2=OR2,
即y2+x2=22,
y=$\sqrt{{2}^{2}-{x}^{2}}$(0<x<$\sqrt{2}$)
点评 考查了勾股定理,矩形的性质,等腰直角三角形的性质,函数关系式,关键是添加辅助线进行求解.

练习册系列答案
相关题目
11.若将分式$\frac{a+b}{2ab}$中的字母a,b的值分别扩大到原来的2倍,则分式的值( )
| A. | 扩大到原来的2倍 | B. | 缩小到原来的$\frac{1}{2}$ | C. | 缩小到原来的$\frac{1}{4}$ | D. | 不变 |
 第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题:
第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题: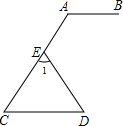 如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.
如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.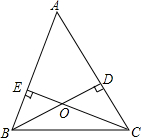 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.