题目内容
20.已知A(-2,2)为正比例函数y=kx上一点,试问在x轴上是否存在一点P,使A,P和坐标原点O构成等腰直角三角形?若存在,试求出P点的坐标;若不存在,试说明理由.分析 过A作AN⊥y轴于N,作AM⊥x轴于M,求出四边形AMON是正方形,求出AN=ON=OM=AM=2,分为两种情况:①∠APO=90°,②∠PAO=90°,求出OP即可.
解答 解:在x轴上存在一点P,使A,P和坐标原点O构成等腰直角三角形,
把A(-2,2)代入y=kx得:k=-1,
即函数的解析式为y=-x,
过A作AN⊥y轴于N,作AM⊥x轴于M,
则∠ANO=∠NOM=∠AMO=90°,
ON=OM=2,
所以四边形AMON是正方形,
即AN=ON=OM=AM=2,
分为两种情况:①如图1,当∠APO=90°时,即P和M重合,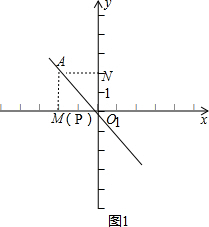
所以此时P的坐标是(-2,0);
②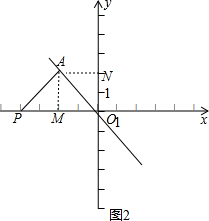
如图2,当∠PAO=90°时,
∵四边形AMON是正方形,
∴∠AOM=∠OAM=45°,
∴∠PAM=45°,
∴∠PAM=∠APM=45°,
∴PM=AM=2,
∴OP=2+2=4,
∴P的坐标是(-4,0);
∵∠AOM=45°,P在x轴上,
∴∠AOP的度数是45°或135°,
即只有以上两种情况,
即P的坐标是(-2,0)或(-4,0).
点评 本题考查了等腰直角三角形的性质,正方形的性质和判定,一次函数的图象上点的坐标特征的应用,能进行分类讨论是解此题的关键.

练习册系列答案
相关题目
11.若将分式$\frac{a+b}{2ab}$中的字母a,b的值分别扩大到原来的2倍,则分式的值( )
| A. | 扩大到原来的2倍 | B. | 缩小到原来的$\frac{1}{2}$ | C. | 缩小到原来的$\frac{1}{4}$ | D. | 不变 |
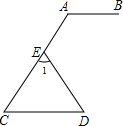 如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.
如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数. 已知圆O,
已知圆O,