题目内容
17.已知二次函数y=x2-2mx+m2+3(m为常数),下列结论正确的是( )| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 | |
| D. | 该函数图象沿y轴向下平移6个单位后,图象与x轴两交点之间的距离为2$\sqrt{3}$ |
分析 根据m=0可得出二次函数图象的顶点坐标为(0,3);根据对称轴公式x=-$\frac{b}{2a}$,抛物线的对称性以及抛物线的平移可得出结论.
解答 解:A、当m=0时,二次函数解析式为y=x2+3,则二次函数图象的顶点坐标为(0,3),故A错误;
B、抛物线对称轴为x=-$\frac{b}{2a}$=m,当m<0时,二次函数图象的对称轴在y轴左侧,故B错误;
C、二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为|m|3,故C错误
D、该函数图象沿y轴向下平移6个单位后,解析式为y=x2-2mx+m2+3-6,即y=x2-2mx+m2-3,与x轴的两个交点为(m+$\sqrt{3}$,0),(m-$\sqrt{3}$,0),两交点之间的距离为2$\sqrt{3}$,故D正确;
故选D.
点评 本题考查了二次函数的性质,涉及到二次函数的解析式,顶点,对称轴以及与坐标轴的交点,难度中等,要熟练掌握.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
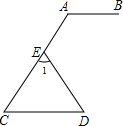 如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.
如图,AB∥CD,∠A=120°,∠1=72°,求∠D的度数.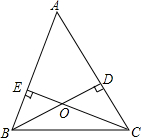 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O. 如图,在△ABC中,已知AB=AC,CE⊥BD,CD=CB,求证:
如图,在△ABC中,已知AB=AC,CE⊥BD,CD=CB,求证: