题目内容
2.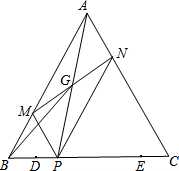 等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.
分析 求出四边形AMPN是平行四边形,根据平行四边形的对角线互相平分可得G是AP的中点,然后判断出点G的运动路线是△APP′的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出GG′,再根据等边三角形的性质求出△BGG′的底边GG′上的高,然后根据三角形的面积公式列式计算即可得解.
解答 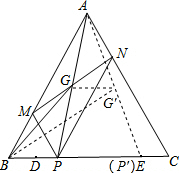 解:∵PM∥AC,PN∥AB,
解:∵PM∥AC,PN∥AB,
∴四边形AMPN是平行四边形,
∵MN与AP相交于点G,
∴G是AP的中点,
∴如图点G的运动路线是△APP′的中位线,
∵BC=6,BD=CE=1,
∴GG′=$\frac{6-1-1}{2}$=2,
∵BC=6,
∴△BGG′的底边GG′上的高=$\frac{1}{2}$×(6×$\frac{\sqrt{3}}{2}$)=$\frac{3\sqrt{3}}{2}$,
∴线段BG扫过的区域面积=$\frac{1}{2}$×2×$\frac{3\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查了点的轨迹,等边三角形的性质,平行四边形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于确定出点G的运动轨迹从而确定出BG扫过的区域是三角形.

练习册系列答案
相关题目
11.2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大了建设资金的投入.
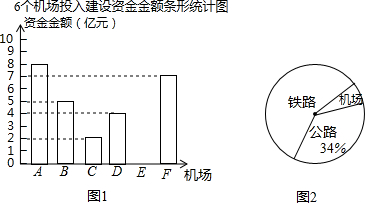
(1)机场建设项目中所有6个机场投入的建设资金金额统计如图1,已知机场E投入的建设资金金额是机场C,D所投入建设资金金额之和的三分之二,求机场E投入的建设资金金额是多少亿元?并补全条形统计图;
(2)将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表,根据扇形统计图及统计表中信息,求得a=170,b=30,c60%,d122.4°,m=500.(请直接填写计算结果)

(1)机场建设项目中所有6个机场投入的建设资金金额统计如图1,已知机场E投入的建设资金金额是机场C,D所投入建设资金金额之和的三分之二,求机场E投入的建设资金金额是多少亿元?并补全条形统计图;
(2)将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表,根据扇形统计图及统计表中信息,求得a=170,b=30,c60%,d122.4°,m=500.(请直接填写计算结果)
| 铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
| 投入资金(亿元) | 300 | a | b | m |
| 所占百分比 | c | 34% | 6% | |
| 所占圆心角 | 216° | d | 21.6° |
12.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2有增根,则m的值是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
7.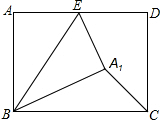 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )| A. | 3或4$\sqrt{2}$ | B. | 3$\sqrt{2}$或4$\sqrt{2}$ | C. | 3或4 | D. | 4或3$\sqrt{2}$ |
14.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( )
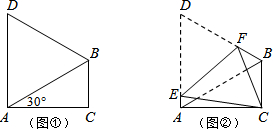

| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
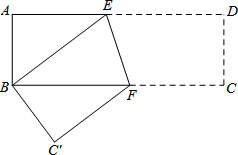 如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( ) 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.