题目内容
17.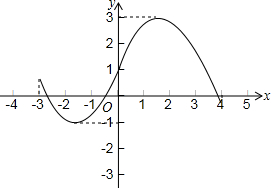 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.例如:下面所表示的函数的界高为4.
(1)若函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围;
(3)已知a>0,函数y=x2-2ax+3a(-2≤x≤1)的界高为$\frac{25}{4}$,求a的值.
分析 (1)将x1=-2代入得:y1=-2k+1,将x2=1代入得:y2=k+1,然后根据|y1-y2|=4,得|-3k|=4,从而可求得k的值;
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,从而可求得m=2;
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1,y2,然后根据|y1-y2|=4,可求得a的值;当0≤a≤1时,将x1=-2,x2=a代入函数的解析式得到y1
、y2,然后根据|y1-y2|=4,可求得a的值.
解答 解:(1)将x1=-2代入得;y1=-2k+1,将x2=1代入得:y2=k+1,
∵|y1-y2|=4,
∴|-3k|=4.
解得:k=$±\frac{4}{3}$.
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
∴m=2.
∴m的取值范围是0≤m≤2.
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1=4+7a,y2=1+a,
∵|y1-y2|=$\frac{25}{4}$,
∴3+6a=$\frac{25}{4}$,
解得:a=$\frac{13}{24}$
又∵a≥1
故此种情况不成立;
当0≤a≤1时,将x1=-2,x2=a代入函数解析式得:y1=4+7a,y2=3a-a2,
∵y1-y2=$\frac{25}{4}$,
∴a2+4a-$\frac{9}{4}$=0,
解得:a1=$\frac{1}{2}$,a2=$-\frac{9}{2}$(舍去)
故a=$\frac{1}{2}$.
点评 本题主要考查的是一次函数和二次函数的性质,根据一次函数和二次函数的增减性以及界高的定义得到相应的方程是解题的关键.

练习册系列答案
相关题目
7.某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
| 时间(第x天) | 1 | 3 | 6 | 10 | … |
| 日销售量(m件) | 198 | 194 | 188 | 180 | … |
| 时间(第x天) | 1≤x<50 | 50≤x≤90 |
| 销售价格(元/件) | x+60 | 100 |
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
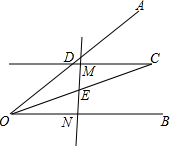 如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论. (1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.
(1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心. 如图,△ABC绕点C旋转后,顶点A旋转到了点A′,画出旋转后的三角形并指出一个旋转角.
如图,△ABC绕点C旋转后,顶点A旋转到了点A′,画出旋转后的三角形并指出一个旋转角.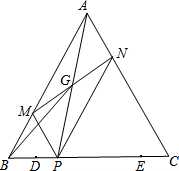 等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.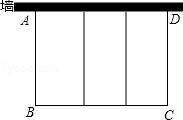 如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.
如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.