题目内容
11. 如图,已知∠E=∠F,∠BAE=∠ABF,求证:0E=0F.
如图,已知∠E=∠F,∠BAE=∠ABF,求证:0E=0F.
分析 根据已知条件证得∠ABE=∠BAF,推出△ABE≌△ABF,根据全等三角形的性质得到AE=BF,得到△AEO≌△BFO,根据全等三角形的性质即可得到结论.
解答 证明:∵∠E=∠F,∠BAE=∠ABF,
∴∠ABE=∠BAF,
在△ABE和△ABF中,
$\left\{\begin{array}{l}{∠E=∠F}\\{∠ABE=BAF}\\{AB=BA}\end{array}\right.$
∴△ABE≌△ABF,
∴AE=BF,
在△AEO和△BFO中,
$\left\{\begin{array}{l}{∠E=∠F}\\{∠AOE=∠BOF}\\{AE=BF}\end{array}\right.$,
∴△AEO≌△BFO,
∴OE=OF.
点评 本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.如果分式$\frac{x-3}{2x+1}$有意义,则x的取值范围是( )
| A. | x≠3 | B. | x$≠-\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=3 |
19.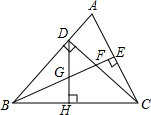 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )| A. | ①③ | B. | ③④ | C. | ①③④ | D. | ①②③④ |
6. 观察表格:
观察表格:
根据表格解答下列问题:
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.
 观察表格:
观察表格:| X | 0 | 1 | 2 |
| ax | 0 | 1 | 2 |
| ax2+bx+c | -3 | -4 | -3 |
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.
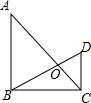 将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.
将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.