题目内容
1.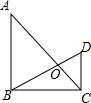 将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.
将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.
分析 根据特殊锐角三角函数值可知:$\frac{AB}{DC}=\frac{\sqrt{3}}{1}$,然后可证明△AOB∽△DOC,最后根据相似三角形的面积比等于相似比的平方求解即可.
解答 解:∵∠D=60°,∠DCB=90°,
∴∠DBC=30°.
∴$\frac{DC}{BC}$=$\frac{\sqrt{3}}{3}$.
∵∠A=45°,∠ABC=90°,
∴∠BCA=∠A=45°.
∴AB=BC.
∴$\frac{DC}{AB}=\frac{\sqrt{3}}{3}$.
∵∠ABC=∠DCB=90°,
∴AB∥CD,
∴△AOB∽△DOC.
∴$\frac{{S}_{△AOB}}{{S}_{△DOC}}=(\frac{AB}{CD})^{2}=3$:1.
故答案为:3:1.
点评 此题考查了相似三角形的判定与性质与三角函数的知识.此题难度不大,解题的关键是数形结合思想的应用与似三角形的面积比等于相似比的平方定理的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.对抛物线y=-2x2+4x-3而言,下列结论正确的是( )
| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与x轴的交点坐标是(0,3) | D. | 顶点坐标是(1,-1) |
10.下列计算中,正确的是( )
| A. | 3a+2b=5ab | B. | 13x-18x=-5 | C. | 5+a=5a | D. | 6ab-ab=5ab |
11.下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中是轴对称图形的有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知∠E=∠F,∠BAE=∠ABF,求证:0E=0F.
如图,已知∠E=∠F,∠BAE=∠ABF,求证:0E=0F.