题目内容
15. 如图,点A与点B分别在函数y=$\frac{k_1}{x}({k_1}>0)$与y=$\frac{k_2}{x}({k_2}<0)$的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是( )
如图,点A与点B分别在函数y=$\frac{k_1}{x}({k_1}>0)$与y=$\frac{k_2}{x}({k_2}<0)$的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设A(a,b),B(-a,d),代入双曲线得到k1=ab,k2=-ad,根据三角形的面积公式求出ad+ad=4,即可得出答案.
解答 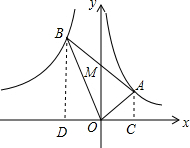 解:作AC⊥x轴于C,BD⊥x轴于D,
解:作AC⊥x轴于C,BD⊥x轴于D,
∴AC∥BD∥y轴,
∵M是AB的中点,
∴OC=OD,
设A(a,b),B(-a,d),
代入得:k1=ab,k2=-ad,
∵S△AOB=2,
∴$\frac{1}{2}$(b+d)•2a-$\frac{1}{2}$ab-$\frac{1}{2}$ad=2,
∴ab+ad=4,
∴k1-k2=4,
故选C.
点评 本题主要考查对反比例函数系数的几何意义,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,能求出ab+ad=4是解此题的关键.

练习册系列答案
相关题目
5.下列命题:①相等的两个角是对顶角;②若∠1+∠2=180°,则∠1与∠2互为补角;③同旁内角互补;④垂线段最短;⑤同角或等角的余角相等;⑥经过直线外一点,有且只有一条直线与这条直线平行,其中假命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列各数中,最小的数是( )
| A. | -$\sqrt{5}$ | B. | -(-3) | C. | |-2| | D. | -π |
 如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.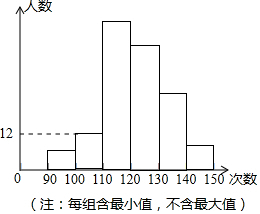 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图(注:每组含最小值,不含最大值).甲同学计算出第二组的频率是0.06,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图(注:每组含最小值,不含最大值).甲同学计算出第二组的频率是0.06,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题: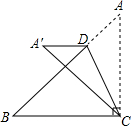 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.
如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.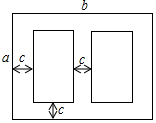 如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.