题目内容
7.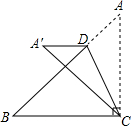 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.
如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.
分析 由等腰直角三角形的性质和勾股定理得出AB=4$\sqrt{2}$,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,根据折叠的性质得到∠A′=∠A=∠A′CB=45°,A′D=AD=x,推出A′C⊥AB,求得BH=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{2}$,DH=$\frac{\sqrt{2}}{2}$A′D=$\frac{\sqrt{2}}{2}$x,然后列方程即可得到结果,②如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD=∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=2.
解答 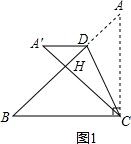 解:Rt△ABC中,BC=AC=4,
解:Rt△ABC中,BC=AC=4,
∴AB=4$\sqrt{2}$,∠B=∠A′CB=45°,
①如图1,当A′D∥BC,设AD=x,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴∠A′=∠A=∠A′CB=45°,A′D=AD=x,
∵∠B=45°,
∴A′C⊥AB,
∴BH=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{2}$,DH=$\frac{\sqrt{2}}{2}$A′D=$\frac{\sqrt{2}}{2}$x,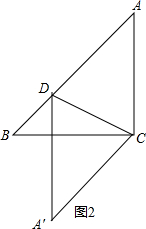
∴x+$\frac{\sqrt{2}}{2}$x+2$\sqrt{2}$=4$\sqrt{2}$,
∴x=4$\sqrt{2}$-4,
∴AD=4$\sqrt{2}$-4;
②如图2,当A′D∥AC,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=4,
综上所述:AD的长为:4$\sqrt{2}$-4或4.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的性质,熟练掌握折叠的性质是解题的关键.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | 购买一张彩票,中奖 | |
| B. | 在标准状况下,加热到100℃时,水沸腾 | |
| C. | 任意画一个三角形,其内角和是360° | |
| D. | 射击运动员射击一次,命中靶心 |
| A. | (2a-1)2=4a2-1 | B. | 3a6÷3a3=a2 | C. | (-ab2)4=-a4b6 | D. | -2a+(2a-1)=-1 |
 如图,点A与点B分别在函数y=$\frac{k_1}{x}({k_1}>0)$与y=$\frac{k_2}{x}({k_2}<0)$的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是( )
如图,点A与点B分别在函数y=$\frac{k_1}{x}({k_1}>0)$与y=$\frac{k_2}{x}({k_2}<0)$的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是( )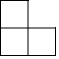 某几何体使用完全相同的正方体搭成的,这个几何体的主视图、俯视图和左视图均是如图所示的图形,则组成该几何体的正方体的个数为( )
某几何体使用完全相同的正方体搭成的,这个几何体的主视图、俯视图和左视图均是如图所示的图形,则组成该几何体的正方体的个数为( ) 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$.
如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$.