题目内容
8.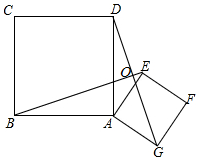 如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
如图,已知正方形ABCD和正方形AEFG,连结BE、DG.(1)求证:BE=DG,BE⊥DG;
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,求证:△MPN是等腰直角三角形;
(3)若AB=4,EF=2$\sqrt{2}$,∠DAE=45°,直接写出MN=2$\sqrt{5}$.
分析 (1)根据SAS证明△BEA与△DAG全等,再利用全等三角形的性质证明即可;
(2)利用三角形中位线定理证得△MPN是等腰直角三角形;
(3)过点G作GH垂直于DA的延长线于点H,利用勾股定理得出DG,进一步得出PN,利用勾股定理得出结果.
解答 (1)证明:∵正方形ABCD和正方形AEFG,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG,
∵在△BEA与△DAG中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAG}\\{AE=AG}\end{array}\right.$,
∴△BEA≌△DAG(SAS),
∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)证明:如图,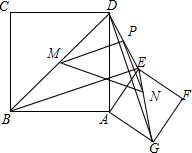
由三角形中位线定理可得:MP∥BE,MP=$\frac{1}{2}$BE,
PN∥DG,PN=$\frac{1}{2}$DG,
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形;
(3)解:如图,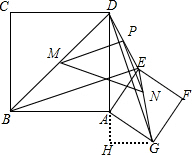
过点G作GH垂直于DA的延长线于点H,
∵∠DAE=45°,∠EAG=90°,
∴∠HAG=45°,
∵EF=2$\sqrt{2}$,
∴AH=HG=2,
∵AB=4,
∴DH=6,
∴DG=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴NP=MP=$\sqrt{10}$,
∴MN=2$\sqrt{5}$.
点评 此题考查三角形全等的判定与性质,三角形的中位线定理,勾股定理,等腰直角三角形的性质,结合图形和数据,灵活作出辅助线解决问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
16. 如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )
如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )
 如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )
如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )| A. | AB=ED | B. | AC=EF | C. | AC∥EF | D. | BC=DF |
13.x2-5x+k中,有一个因式为(x-2),则k的值为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
20.关于x的方程$\frac{x}{x-3}$=2+$\frac{k}{x-3}$会产生增根,那么k的值( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
17.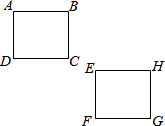 如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
 如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
如图,正方形EFGH是由正方形ABCD平移得到的,则有( )| A. | 点E和B对应 | B. | 线段AD和EH对应 | C. | 线段AC和FH对应 | D. | ∠B和∠D对应 |
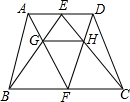 已知,如图,梯形ABCD中,AD∥BC,AD=m,BC=n,E、F分别是AD、BC的中点,AF与BE相交于点G,EC与DF相交于点H.求证:
已知,如图,梯形ABCD中,AD∥BC,AD=m,BC=n,E、F分别是AD、BC的中点,AF与BE相交于点G,EC与DF相交于点H.求证: