题目内容
11.对于四边形ABCD,下面给出对角线的三种特征:①AC、BD互相平分;②AC⊥BD;③AC=BD.当具备上述条件中的①③,就能得到“四边形ABCD是矩形”分析 依据对角线相等的平行四边形是矩形进行判断即可.
解答 解:当具备①③两个条件,能得到四边形ABCD是矩形.
理由:∵对角线AC、BD互相平分,
∴四边形ABCD为平行四边形.
又∵AC=BD,
∴四边形ABCD为矩形.
故答案为:①③.
点评 本题主要考查的是矩形的判定,掌握矩形的判定定理是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.二次函数y=x2-4x-5的图象的对称轴为( )
| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=2 | D. | 直线x=-2 |
19.下列计算错误的是( )
| A. | x2+x4=x6 | B. | 2xy+3xy=5xy | C. | (x3)2=x6 | D. | x6÷x3=x3 |
3.如果一个平行四边形的两条对角线相等,那么这个四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
20.以下列的各组线段长度为边能组成三角形的是( )
| A. | 1、2、4 | B. | 2、3、5 | C. | 8、4、6 | D. | 12、6、5 |
1.某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使利润为6125元,设每件商品应降价x元,则可列方程为( )
| A. | (20+x)(300+20x)=6125 | B. | (20-x)(300-20x)=6125 | ||
| C. | (20-x)(300+20x)=6125 | D. | (20+x)(300-20x)=6125 |
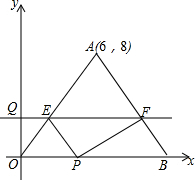 如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.